
 Impressum/Note Datenschutzerklärung
Impressum/Note Datenschutzerklärung|
Pages by Andreas Hofmeier |
 |
 Impressum/Note Datenschutzerklärung Impressum/Note Datenschutzerklärung |
|---|
|
http[s]://www.abmh.de/fhs/crypt/AES2LoopAES/RST_AES.HTML/index.html |
|---|
| Betreuer: | Prof. Dr. Thomas Risse |
| Studiengang: | ESTI, 7. Semester |
| Martrikelnummer: | 94453 |
|
Zusammenfassung Im ersten und zweiten Abschnitt dieses Dokumentes wird eine Übersicht
über die Grundlagen der Kryptographie gegeben. Es werden Summen-,
Permutations- und Substitutionsverfahren erklärt.
|
Kryptographie1 bezeichnet Verfahren, welche entwickelt wurden, um Informationen vor unbefugtem Zugriff zu schützen. Dies ist notwendig, da es in der digitalen Welt möglich ist, Daten ohne nennenswerten Aufwand zu vervielfältigen. Dies hinterlässt im Allgemeinen keine Spuren an den Daten. Soll ein öffentliches Netzwerkes zur Datenübertragung genutzt werden, ist der Einsatz von Kryptographie anzuraten, da es nicht möglich ist, seine Nachricht in einen Briefumschlag zu stecken. Heutige Datennetzwerke sind eher mit dem Versand von Postkarten zu vergleichen: Jeder, der sich in den Weg der Postkarte (oder der Datenübertragung) einklinken kann, ist in der Lage mitzulesen. Wie bereits erwähnt, entstehen dabei keine Spuren an den übermittelten Daten.
Um eine Nachricht vor den Augen Neugieriger zu schützen, wandelt Kryptographie die Nachricht mit Hilfe eines mathematischen Verfahrens in die Chiffre2 um. Wer die Nachricht lesen will, muss über ein Verfahren verfügen, welches diese Umwandlung rückgängig macht.
Soll sichergestellt werden, dass nur ein einziger Empfänger die Nachricht lesen kann, müssen sich Sender und Empfänger ein einzigartiges mathematisches Verfahren teilen. Es wäre sehr aufwendig, so viele mathematische Verfahren zu entwickeln und auf Sicherheit hin zu überprüfen. Aus diesem Grund wird das mathematische Verfahren so gestaltet, dass es von einem weiteren Parameter abhängig ist: dem Schlüssel. Die gleiche Nachricht, mit dem selben Verfahren aber mit unterschiedlichen Schlüsseln verschlüsselt, führt zu verschiedenen Chiffren. Um die Nachricht lesen zu können, muss auf der Empfängerseinte nicht nur das Verfahren, sondern auch der Schlüssel bekannt sein.
Diese Klasse von Verfahren wird als symmetrische Verschlüsselung bezeichnet, da zum Ver- und Entschlüsseln derselbe Schlüssel verwendet wird.
Von der symmetrischen Verschlüsselung wird die unsymmetrische Verschlüsselung unterschieden. Eine weiterführende Einführung in die Grundprinzipien der Kryptographie (symmetrische und unsymmetrische Verschlüsselung) wird unter http://www.abmh.de/fhs/crypt/DerTunnel/DerTunnel.PDF.pdf gegeben.
Diese Dokument beschäftigt sich dagegen mit AES, dem Advanced Encryption Standard, einem Standardverfahren zur symmetrischen Verschlüsselung.
Bei dem Summenverfahren werden der Klartext und der Schlüssel aufsummiert um die Chiffre zu erhalten. Die Chiffre wird wieder lesbar gemacht, indem der Schlüssel von der Chiffre abgezogen wird.
Beispiel:
| 6124627 |
| +4531773 |
| 10656400 |
Ergebnis: Chiffre (10656400)
| 10656400 |
| -4531773 |
| 6124627 |
Ergebnis: Klartext (6124627)
Das Aufsummieren von Nachrichten gestaltet sich im allgemeinem schwieriger. Der Grund dafür ist, dass Nachrichten bzw. Daten normalerweise nicht als “eine Zahl” vorliegen, sondern wesentlich komplexere Strukturen aufweisen. So werden Nachrichten meist in Sprache formuliert. Diese Sprache besteht aus Sätzen, welche wiederum aus Wörtern bestehen. Wörter ihrerseits bestehen aus Buchstaben. In Computern werden Daten (also auch Nachrichten) auf unterster Ebene als Byte Strings (Aneinanderreihungen von Zeichen) behandelt. Solch ein Byte String kann mathematisch als Zahl aufgefasst werden. Praktisch übersteigt die größer dieser Zahl schnell alle technisch handhabbaren Dimensionen. Daher wird bei der Verschlüsselung nicht der gesamte Byte String als Zahl betrachtet, sondern jedes Byte für sich alleine.
Beispiel:
|
Die folgenden Annahmen werden getroffen, um die Nachricht verschlüsseln zu können:
|
Wie im Beispiel zu erkennen ist, ergeben sich bei einigen Additionen Werte über 26. Diese können scheinbar keinem Buchstaben zugeordnet werden. Diese Problem tritt auf, da die Menge an Buchstaben, denen Zahlen zugeordnet werden können, beschränkt ist. Dagegen ist die Menge der ganzen Zahlen nicht begrenzt.
Diese Problem kann umgangen werden, indem der Zahlenraum nicht als unendlicher Zahlen-Strahl, sondern als begrenzter Zahlen-Kreis aufgefasst wird. Dieser Kreis verbindet das künstliche Ende des Zahlenstrahls (26) mit seinem Anfang (0).
|
Eine Addition von 27 führt im Zahlenkreis wieder auf den Ausgangswert. Auf das Beispiel bezogen Heißt das, dass ab 26 mit 0 hätte weitergezählt werden müssen. Der Schritt (1) im Beispiel realisiert dies mit Hilfe der modulo27-Operation. modulo27 gibt den (ganzzahligen) Divisionsrest der Division einer ganzer Zahlen durch 27 zurück. Diese Operation kann nachgebebildet werden, indem sooft 27 abgezogen wird, bis das Ergebnis kleiner als 27 ist. Nach der Operation (1) können alle Zahlen wieder Buchstaben zugeordnet werden.
Soll die Chiffre entschlüsselt werden, müssen die entgegengesetzten Rechenoperationen durchgeführt werden. Im Beispiel heißt dies, den Schlüssel von der Chiffre abzuziehen. Dazu werden den Buchstaben erneut Zahlen zugewiesen, welche dann voneinander subtrahiert werden können. Auch bei dieser Operation entsteht das Problem des begrenzten Zeichenvorrats, dem wieder durch modulo27 abgeholfen wird. Diese Operation (2) kann nachgebildet werden, indem solange 27 zu dem Ergebnis hinzuaddiert wird, bis dieses größer als 0 ist.
|
Der begrenzte Zahlenraum ist nicht nur eine Annahme in diesem abstrakten Beispiel, sondern eine zentralen Einschränkung jeder Rechenmaschine. So basieren alle heutigen Computer auf Bits, welche als Zahlenraum von 0 und 1 aufgefasst werden können.
Diese Bits können zusammengefasst werden, um größere Zahlenräume (komplexere Sachverhalte) darzustellen. Werden acht Bit zu einem Byte zusammengefasst, sind 28 = 256 verschiedene Zahlen darstellbar. Diese werden im so genannten ASCII-Zeichensatz verschiedenen Zeichen (Buchstaben, Zahlen und Sonderzeichen) zugeordnet. Aus diesen Zeichen können nun wieder Texte (Nachrichten) komponiert werden.
Computer arbeiten von Haus aus mit diesen beschränkten Zahlenräumen. Wird auf einem 8-Bit-Rechner die Zahl 254 mit der Zahl 4 addiert, so ist das Ergebnis 2 und nicht wie erwartet 258. Der Grund dafür ist, dass jedes Rechenwerk mit einem begrenztem Zahlenraum arbeitet. Dieser kann als Zahlenkreis aufgefasst werden. Um mitzuteilen, dass der Zahlenraum überschritten wurde, setzt das Rechenwerk im allgemeinem ein Überlauf-Bit. Diese Rechenwerke haben die Eigenschaft, dass Berechnungen auch dann zum Richtigen Ergebnis führen, wenn Zwischenergebnisse den Begrenzte Zahlenraum verlassen. Das Ergebnis muss sich allerdings wieder im Zahlenraum darstellen lassen.
Das folgende Beispiel zeigt, wie jedes Bit eines Bytes einzeln addiert wird. Es wird also nicht die gesamte Zahl, bestehend aus acht Bit, addiert, sondern die Bits unabhängig voneinander:
|
Auf Grund der Symmetrie ist die Rechenoperation (1) und (2) in diesem Beispiel identisch. Die Addition zweier Bits mit anschließender Operation (1) ist eine weitläufig bekannte Rechenoperation in Computern: Die XOR oder Exklusiv-Oder-Operation. XOR kommt auch heutzutage bei Verschlüsselung sehr häufig zum Einsatz.
Das Permutationsverfahren stellt eine weitere Möglichkeit dar, Nachrichten zu verschlüsseln. Bei diesem Verfahren werden die Positionen der Zeichen verändert, nicht aber die Zeichen selber. Dies kann beispielsweise erreicht werden, indem die Nachricht von rechts nach links und von oben nach unten in eine Matrix geschrieben wird und danach von oben nach unten und von rechts nach links wieder herausgelesen wird.
|
Natürlich sind alle möglichen Formen von “Matrizen” und Aus- bzw. Einlesemustern vorstellbar. Deters (2002) beschreibt zum Beispiel eine historische Anwendung dieses Verfahrens: Die Regierung von Sparta zur hat bereits 500 v. Chr. mit Hilfe eines Holzstabes (Skytale) verschlüsselt. Die Nachricht wurde vom Sender der Länge nach auf einen mit einem Pergamentsteifen umwickelten Holzstab geschrieben. Danach wurde das Pergament abgewickelt, nochmals abgeschrieben und versandt. Der Empfänger musste nun die empfangene Nachricht auf einen Pergamentstreifen schreiben und diesen um einen Holzstab mit dem richtigen Durchmesser wickeln, um die Nachricht zu entschlüsseln.
|
Beispiel einer historischen Verschlüsselung. Übernommen von Deters (2002).
Das Substitutionsverfahren ersetzt Elemente der Nachricht nach bestimmten Regeln gegen andere Elemente. Deters (2002) führt hier das älteste bekannte Beispiel einer Verschlüsselung auf: die Cäsar-Chiffre. Diese Methode ist nach Cäsar benannt. Er schrieb das Alphabet zweimal untereinander, wobei er es beim zweiten Mal um drei Buchstaben nach rechts einrückte. (Das Lateinischen Alphabet verfügt nicht über die Buchstaben J, K, W, Y und Z.):
A B C D E F G H I L M N O P Q R S T U V X
U V X A B C D E F G H I L M N O P Q R S T
Übernommen von Deters (2002).
Um eine Nachricht zu verschlüsseln, werden alle Zeichen der Nachricht durch das korrespondierende Zeichen ersetzt:
TREFFEN UM SIEBEN ← Klartext
QOBCCBI RH PFBVBI ← Chiffre
AES ist der in einem öffentlichen Auswahlverfahren vom NIST3 bestimmte Nachfolger von DES (Data Encryption Standard). Ein neuer Standard für Datenverschlüsselung wurde notwendig, da es laut Wilkin (2004) der Electronic Frontier Foundation 1998 gelungen war, eine Maschine zu bauen, die DES mittels einer Brute-Force-Attack aushebeln konnte. Im Gegensatz zu DES war die Auswahl von AES vollständig öffentlich. Jeder Interessierte konnte seinen Vorschlag in Form eines Verschlüsselungsalgorithmus einschicken oder sich an dem Test der Algorithmen beteiligen. Die NIST suchte den besten Algorithmus aus, wobei folgende Kriterien in Betracht gezogen wurden:
Die folgende Tabelle gibt eine Übersucht über alle Algorithmen, welche für den neuen Verschlüsselungsstandard AES vorgeschlagen wurden, von wem sie vorgeschlagen wurden und in welcher Runde sie ausgeschieden sind.
| Name | eingereicht von | ausge. Runde | ||
| CAST-256 | Entrust (CA) | Company | 11 | |
| Crypton | Future Systems (KR) | Company | 12 | |
| DEAL | Outerbride, Knudsen (USA-DK) | Forscher | 1sp | |
| DFC | ENS-CNRS (FR) | Forscher | 13 | |
| E2 | NTT (JP) | Company | 14 | |
| Frog | TecApro (CR) | Company | 1s | |
| HPC | Schroeppel (USA) | Forscher | 1s | |
| LOKI97 | Brown et al. (AU) | Forscher | 1s | |
| Magenta | Deutsche Telekom (DE) | Company | 1sp | |
| Mars | IBM (USA) | Company | 2 | |
| RC6 | RSA (USA) | Company | 2 | |
| Rijndael | Daemen and Rijmen (BE) | Forscher | WINNER | |
| SAFER+ | Cylink (USA) | Company | 1p | |
| Serpent | Anderson, Biham, Kundsen (UK-IL-DK) | Forscher | 2 | |
| Twofish | Counterpane (USA) | Company | 2 | |
Adaptiert von Daemen und Rijmen (2002).
1) Ausgeschieden in der ersten Runde. Auswahl der fünf Finalisten im März
1999.
2) Ausgeschieden in der zweiten Runde, Endausscheidung am 2. Oktober
2000
s) Ausscheidung wegen massiver Sicherheitsprobleme
p) Ausscheidung wegen massiver Leistungsprobleme
1) Vergleichbar mit Serpent, Implementation aufwendiger.
2) Vergleichbar mit Rijndael und Twofish aber unsicherer.
3) Geringe Sicherheit, schlechte Performance außer auf 64-Bit Prozessoren.
4) Vergleichbar mit der Struktur von Rijndael und Twofish, aufwendigere
Implementation
Alle Kandidaten mussten bis zum 15. Mai 1998 eingereicht werden. Am 20. August begann dann die erste Runde, welche im März 1999 mit der Auswahl der fünf Finalisten endete. Am 2. Oktober 2000, nach einer weiteren Auswahl-Runde, wurde schließlich der Gewinner gekürt: Rijndael. Von nun an als AES bezeichnet. Dieser Algorithmus wurde Joan Daemen und Vincent Rijmen, zwei belgischen Wissenschaftlern, als Kandidat für die AES-Ausschreibung entwickelt.
Viele Beobachter waren darüber erstaunt, dass ein Algorithmus gewonnen hat, der weder aus den USA stammt noch von einer Firma aus dem Verschlüsselungsgeschäft entwickelt wurde. Von vielen Seiten wurde aus diesem Grund auf ein objektives Auswahlverfahren geschlossen, welches am Schluss den besten Algorithmus zum Gewinner kürte.
Die grundlegende Struktur des AES-Algorithmus ist in der folgenden Weise aufgebaut:
Adaptiert von Daemen und Rijmen (2002).
Daemen und Rijmen (2002) betrachten Blöcke in der folgenden Weise. Es werden jeweils vier Bytes von oben nach unten geschrieben. Beim fünften Byte wird nach rechts weitergegangen und wieder oben angefangen.
|
In der folgenden graphischen Darstellung wird von einer Blockgröße von 128 Bit ausgegangen. Die Blöcke ließen sich allerdings in Vier-Byte-Schritten (32 Bit) bis auf 256 Bit ausweiten. Dasselbe gilt für den Schlüssel. Daten-Blockgröße und Schlüssel-Block-Größe sind vollkommen unabhängig voneinander. Im AES-Standard sind allerdings lediglich Datenblockgrößen von 128 Bit und Schlüsselblocklängen von 128, 192 und 256 Bit vorgesehen. Dies ändert nichts daran, dass der Rijndael-Algorithmus mehr kann, was aber nicht notwendiger implementiert sein muss, wenn auf AES Bezug genommen ist.
Die graphische Darstellung verdeutlicht den Fluss der Daten:
|
Adaptiert von Daemen und Rijmen (2002).
Wie oben ersichtlich, wird die Funktion Round() N mal ausgeführt. Wobei N von der Schlüssel- und der Daten-Block-Größe abhängt. Die folgende Tabelle stellt die Länge des Schlüssels der Länge des Datenblockes gegenüber und gibt für jede Kombination eine Anzahl von Runden an. Alle fett dargestellten Fälle sind durch den AEStandard definiert. Die restlichen Fälle werden von Rijndael unterstützt, sind aber im Standard nicht definiert.
| Länge des Datenblockes | 128 | 160 | 192 | 224 | 256 |
| 128 | 10 | 11 | 12 | 13 | 14 |
| 160 | 11 | 11 | 12 | 13 | 14 |
| 192 | 12 | 12 | 12 | 13 | 14 |
| 224 | 13 | 13 | 13 | 13 | 14 |
| 256 | 14 | 14 | 14 | 14 | 14 |
Vor der ersten und nach jeder Runde wird der Datenblock mit einem gleich großen Schlüsselblock geXORt. Dies wird mit Hilfe der Funktion AddRoundKey() durchgeführt. Die XOR-Funktion kann als eine Form des Summenverfahrens angesehen werden, welche im Abschnitt 2.1 behandelt wurde.
Die Funktion KeyExpansion() wurde implementiert, um den Schlüssel auf die richtige Länge zu erweitern. Denn sowohl der Schlüssel als auch der Datenblock können verschiedene, voneinander unabhängige, Längen aufweisen. Die Funktion erweitert die Länge des Schlüssels auf (Runden + 1) * Daten-Blockgröße, da vor der ersten und nach jeder Runde einmal ein Teil-Schlüssel von der Länge des Datenblockes gebraucht wird. Die hinzugefügten Bytes werden durch ein reproduzierbares mathematisches Verfahren erzeugt, welches recht unvorhersagbare vom Schlüssel abhängige Werte liefert. Diese Funktion kann mit einem Pseudo-Zufallszahlen-Generator verglichen werden. Derselbe Startwert führt immer zu der selben Abfolge von Zahlen, welche aber möglichst zufällig sein soll. So wird ein 128-Bit-Schlüssel auf den richtigen Wert (Hier: (Runden + 1) * Daten-Blockgröße) erweitert:
Der hier aufgeführte erweiterte Schlüssel entsteht, wenn der übergebende Schlüssel aus Nullen (alle Bits sind Null) besteht.
Den Autor hat es verwundert, dass der Schlüssel nicht verwendet wurde, um die verändernden Funktionen (SubBytes(), ShiftRows() und MixColums()) direkt zu steuern. Stattdessen werden diese Funktionen immer in der gleichen Weise auf den Datenstrom abgewendet. Die Abhängigkeit vom Schlüssel wird über die Funktion AddRoundKey() eingeführt.
Die Funktion ShiftRows() wendet ein Permutationsverfahren (siehe Abschnitt 2.2) auf den Datenstrom an. In diesem Fall wird der Block zeilenweise betrachtet. Bis auf die oberste wird jede Zeile um n Spalten nach links verschoben. Die Weite der Verschiebung hängt von der Blockgröße und der Zeile ab.
Die folgende Tabelle stellt die (Daten)Blockgröße mit den Zeilen gegenüber und gibt für jede Paarung einen Wert für die Linksverschiebung an. Im AEStandard ist lediglich der Fall des 128-Bit-Blocks definiert. Da der Rijndael-Algorithmus mit größeren Blöcken umgehen kann, ist dies hier ebenfalls aufgeführt.
| Zeile | 128 | 160 | 192 | 224 | 256 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 1 | 1 | 1 |
| 3 | 2 | 2 | 2 | 2 | 3 |
| 4 | 3 | 3 | 3 | 4 | 4 |
Die folgende Graphik versucht dies am Beispiel eines 128Bit Blockes zu verdeutlichen.
|
Die inverse Funktion (InvShiftRows()) schiebt die Zeilen um die gleiche Anzahl von Bytes in die entgegengesetzte Richtung.
Die Funktionen SubBytes() und MixColums() wenden eine Form von Substitutionsverfahren (siehe Abschnitt 2.3) auf den Datenstrom an. Es besteht jedoch ein grundlegender Unterschied zu den in Abschnitt 2.3 beschriebenden Substitutionsverfahren. Die Substitution wird nicht wie beschrieben durch den Schlüssel bestimmt, sondern ist fest vorgegeben. Wie bereits erwähnt, wird die Abhängigkeit vom Schlüssel durch die XOR-Schritte bewirkt.
SubBytes() verarbeitet jedes Byte im Datenblock einzeln.
|
Adaptiert von Daemen und Rijmen (2002).
Es wird ein “Alphabet” von mit 256 (28 da 8Bit) Symbolen verwendet. Jedes der Symbole wird durch ein anderes Symbol (ebenfalls Teil des Alphabets) ersetzt. Dies Substitution ist durch den folgenden mathematischen Zusammenhang bestimmt:
Zuerst werden die Bits (a7 bis a0) in dem Byte (a) als Polynom betrachtet:
a = a7a6a5a4a3a2a1a0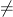 0 ⇒ f(x) = a7x7 + a
6x6 + a
5x5 + a
4x4 + a
3x3 + a
2x2 + a
1x+a
0
0 ⇒ f(x) = a7x7 + a
6x6 + a
5x5 + a
4x4 + a
3x3 + a
2x2 + a
1x+a
0
Danach wird die Inverse dieses Polynoms gebildet. Diese Operation wird in GF(28) = GF(256) ausgeführt.
g(x) = f(x)-1
Dann wird das so gewonnene Polynom wieder in ein Byte zurückgewandelt:
g(x) = b7x7 + b 6x6 + b 5x5 + b 4x4 + b 3x3 + b 2x2 + b 1x+b 0 ⇒ b = b7b6b5b4b3b2b1b0
Für den nicht definierten Fall, dass a gleich 0 ist, wird angenommen, dass b ebenfalls 0 ist.
Danach werden die Bits des Bytes als Vektor betrachtet und der folgenden Vektor-Matrix-Multiplikation mit anschließendem XOR unterzogen:
c =  =
=  ×
× ⊕
⊕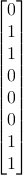
Die InvSubBytes() macht den so eben beschriebenen Vorgang rückgängig. Dazu wird zuerst die Vektor-Matrix-Multiplikation mit anschließendem XOR invertiert durchgeführt:
b =  =
=  ×
× ⊕
⊕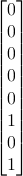
Danach wird das Ergebnis als Polynom betrachtet und invertiert. Dieser Schritt führt auf das originale a zurück.
Im Allgemeinen ist das Nachschlagen eines Wertes schneller als das Errechnen des selbigen. Dies trifft jedenfalls zu, wenn die Tabelle relativ klein ist. Dieses Vorgehen ist ebenfalls eine bei der Implementierung von AES angewendete Alternative zu der eben beschriebenen Rechnung. Denn die Tabelle besteht aus lediglich 256 (28) Einträgen. Praktisch kann die Liste in diesem Fall mit Hilfe eines 256 Byte langen Arrays dargestellt werden. Dazu wird an der jeweiligen Position im Array das zugehörige Ergebnis gespeichert. Wenn, zum Beispiel, die oben beschriebende mathematische Transformation mit einer Eingabe von 2 zu dem Ergebnis 119 führt, so steht an der dritten Stelle des Arrays eine 119. (Es handelt sich um die dritte Stelle, da im Computerbereich bei 0 angefangen wird zu Zählen.) Heiße das Array S, so ergibt sich folgender Zusammenhang:
Wenn die Variable input mit 2 initialisiert wurde, steht nach dem Aufruf dieser Zeile 119 in output. Im Allgemeinen wird dieses Verfahren als Look-Up-Table bezeichnet. Die inverse Transformation funktioniert entsprechend, nur dass das entsprechende Array verwendet wird.
MixColums() wird jeweils auf 4-Bytes-Spalte angewendet. Wird diese Funktion als Substitution betrachtet, besteht das “Alphabet” aus 4 294 967 296 (= 232 = 24*8) Symbolen. Bei dieser Menge an Symbolen ist an eine Verwendung einer Tabelle nicht mehr zu denken.
Die Umwandlung in diesem Schritt ist durch eine Matrix-Vektor-Multiplikation bestimmt. In diesem Fall wird ein Vektor von 4 Bytes mit einer Matrix von 4 × 4 Bytes Multipliziert:
b =  =
=  ×
×
Wobei i der zu verarbeitenden Spalte entspricht. Im Falle eines 128 Bit Blockes sind vier Spalten zu verarbeiten.
|
Adaptiert von Daemen und Rijmen (2002).
Um diese Umwandlung rückgängig zu machen, wurde die Funktion InvMixColums() entwickelt, die folgende mathematische Operation ausführt:
a =  =
= 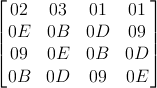 ×
×
Die hier verwendete Matrix kann durch invertieren der in MixColums() verwendeten Matrix errechnet werden.
Um die verschlüsselten Daten wieder in die Ausgangsdaten zurück zu wandeln, wird folgendermaßen vorgegangen: Die Reihenfolge der Schritte wird umgekehrt. Bei jedem Schritt wird der invertierende Schritt angewendet. Zum Beispiel InvMixColums() statt MixColums(). Die folgende Graphik versucht dies deutlich zu machen und stellt dazu den Ver- und Entschlüsselungsprozess gegenüber.
|
Adaptiert von Daemen und Rijmen (2002).
Es wurde gerade davon gesprochen, alle Schritte in umgekehrter Reihenfolge abzuarbeiten. In der Graphik wurden aber zwei Schritte nicht vertauscht. Warum?
Es handelt sich um die letzten beiden Schritte bei der Verschlüsselung oder um die ersten beiden bei der Entschlüsselung: ShiftRows() und SubBytes(), bzw, InvShiftRows() und InvSubBytes(). Dies kann ganz einfach erklärt werden: Es macht keinen Unterschied, ob diese beiden Schritte getauscht sind oder nicht. SubBytes() wird auf jedes Byte einzeln angewendet, daher spielt es keine Rolle, ob ShiftRows() die Bytes vorher oder nachher verschiebt. Diese und andere hier nicht erwähnte Möglichkeiten, die Reihenfolge von Operationen zu vertauschen, werden zur Optimierung der Implementation verwendet.
AES verschlüsselt “nur” 128-Bit-Blöcke. Nur welche Nachrichten bzw. Dateien sind schon 128 Bit (16 Byte) lang?
Es gibt die Möglichkeit, die zu verschlüsselnde Datei oder Nachricht in 128-Bit-Blöcke aufzuteilen. Wird AES auf jeden dieser Blöcke unabhängig angewendet, so nennt man dies das elektronische Code-Buch Verfahren (engl. ECB – Electronic Code Book):
|
Diese Unabhängigkeit der Blöcke führt dazu, dass identische Klartext-Blöcke bei der Verschlüsselung die selben Chiffre-Blöcken ergeben. Die Verschlüsselung könnte als eine Form der Substitution vergleichen werden, nur dass das Alphabet in diesem Fall über 340282366920938463463374607431768211456 = 2128 ≈ 3.4 * 1038 Symbole verfügt. Es wäre also von der Kapazität her nicht möglich, einer Liste mit dieser Menge an Einträgen zu verwalten. Allerdings ist es möglich, häufig auftretende gleiche Blöcke zu identifizieren. Dies ist ein möglicher Angriffspunkt auf die Verschlüsselung.
Um diesem Effekt vorzubeugen, werden die Blöcke im CBC-Mode voneinander abhängig gemacht. Dies geschieht, indem der Input vor der Verschlüsselung mit dem Output der vorherigen Verschlüsselung geXORt wird:
|
Die Chiffre vom aktuellen Klartextblock ist in diesem Fall nicht nur vom Klartextblock und dem Passwort abhängig, sondern zusätzlich vom vorherigen Chiffre-Block. Dieser wiederum ist seinerseits wieder abhängig vom Passwort, vom Klartextblock und vom vorherigen Chiffre-Block. Der erste Chiffre-Block ist seinerseits vom Passwort, dem Klartext-Block und dem IV abhängig. Der IV (Initial Vector) ist ein Anfangswert, welcher als Ersatz für den vorherigen Block mit dem Klartext geXORt wird. Die letzte Chiffre ist allerdings vom Password und von allen vorherigen und dem letzten Klartext abhängig. Aus diesem Grund könnte die letzte Chiffre auch als HASH-Wert des Datenstromes betrachtet werden.
Nachteile dieser beiden Lösungen sind, dass
Ein andere Möglichkeit ist, den Verschlüsselungsalgorithmus zu verwenden, um einen Schlüsselstrom zu erzeugen. Die zu verschlüsselnden Daten werden danach mit diesem Schlüsselstrom geXORt und somit verschlüsselt:
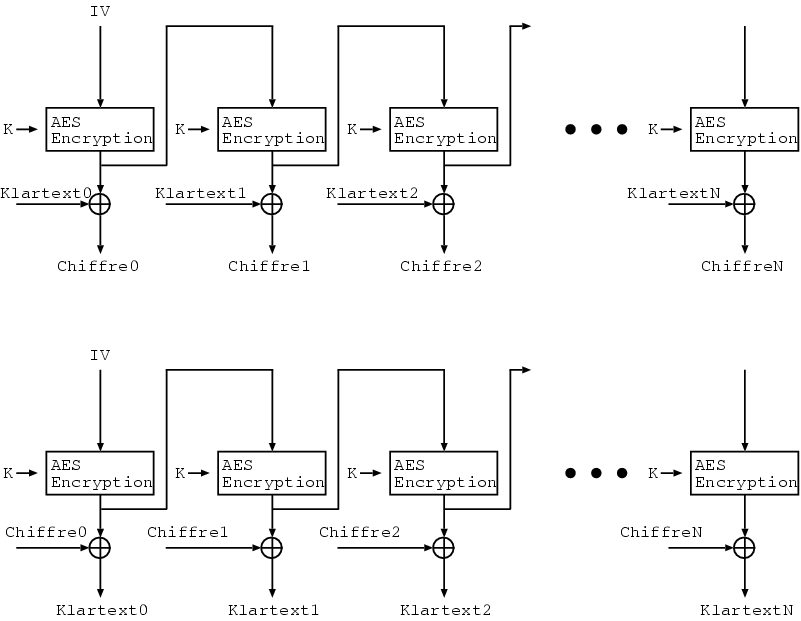 |
Vorteil dieser Variante ist, dass die Länge der Nachricht kein Vielfaches von der Blockgröße sein muss. Denn der letzte Block muss nicht vollständig sein. Ist der Block nur ein Byte lang, so kann dieses Byte mit dem ersten Byte aus dem aktuellen Keystream-Block verschlüsselt werden. Die restlichen Bytes des Keystream-Blocks bleiben dabei einfach ungenutzt.
Der Loop5-Driver unter Linux wurde entwickelt, um normale Dateien oder andere Blockdevices6 als virtuelle Blockdevices abzubilden. Dies ist notwendig, wenn ein Image7 gemountet8 werden soll. Auf Grund der blockorientierten Struktur kann eine Datei nicht direkt gemountet werden.
Die folgende Graphik versucht diesen Zusammenhang nochmals zu verdeutlichen.
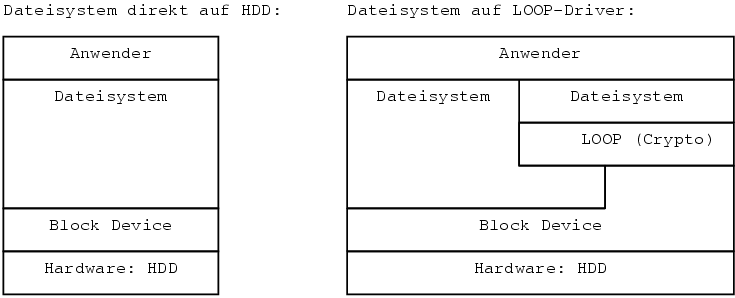 |
Auf der linken Seite ist die “normale” Zugriffsstruktur abgebildet: Der Anwender greift auf das Dateisystem zu, welches in ein Verzeichnis gemountet ist. Das Dateisystem seinerseits verwendet die Blockdevices als Schnittstelle zur Hardware. Rechts wurde diese Struktur um ein virtuelles Blockdevice (Loop-Device) erweitert. Das Dateisystem, welches auf das virtuelles Blockdevice zugreift, sieht keinen Unterschied zu einem “normalem” Blockdevice (Außer den Namen: /dev/loop). Dieses virtuelles Blockdevice kann seinerseits auf ein anderes Blockdevice oder auf eine Datei in einem bereits gemounteten Dateisystem zugreifen. Der erste Fall scheint auf den ersten Blick sinnlos zu sein. Dies ist er allerdings ganz und gar nicht, da der Loop-Treiber noch ein bisschen mehr leisteten kann, als ein Blockdevice zu emulieren. Es kann nämlich ein Offset9 schalten und verschlüsseln. Im folgenden wird auf die zweite Erweiterung näher eingegangen.
Der Crypto-Loop-Driver arbeitet mit einer Blockgröße von 512 Bytes. Soll ein Dateisystem verwendet werden, welches kein Vielfaches dieser Blockgröße verwendet, sind Performanceeinbußen zu erwarten. Das selbe gilt, wenn Offsets kein Vielfaches von 512 sind.
Auf jeden 512-Byte Block wird der Verschlüsselungsalgorithmus im CBC-Mode unabhängig angewendet. Seit dem Kernel 2.6 ist AES im Loop-Treiber offiziell integriert.
Bei der Verwendung von Journaling Dateisystemen mit Crypto-Loop ist Vorsicht geboten, da Schreibzugriffe möglicherweise nicht sofort durchgeleitet werden. Dies wird von einem Journaling Dateisystemen aber normalerweise gefordert. Es gibt allerdings die Möglichkeit, dieses Problem zu umgehen. Bei den weiter unten beschriebenen Versuchen wurde tatsächlich festgestellt, dass Daten auch nach einem sync10 nicht immer sofort zurückgeschrieben wurden. Das Problem liegt hierbei in der mehrfach gepufferten Struktur, denn gepuffert wird vom Dateisystem und vom Crypto-Loop-Treiber.
Um maximale Geschwindigkeit zu erreichen, wurde der AEStandard für Intel x86 und AMD64 Prozessoren in Assembler implementiert. Diese Optimierung kann allerdings nur auf diesen beiden Prozessoren verwendet werden. Wird Linux auf einer anderen Plattform übersetzt, wird der “normale” C-Code compiliert.
Wie bereits erwähnt, wurde Crypto-Loop im 2.6er Kernel offiziell aufgenommen. Dies bedeutet, dass der Loop-Treiber AES unterstützt11. Zusätzlich können folgende Algorithmen geladen werden: Twofish, Blowfish, Serpent, Mars, rc6, und TripleDES.
Bevor mit der Installation begonnen wird, ist es auf jeden Fall sinnvoll zu überprüfen, ob der aktuelle Kernel nicht doch schon Crypto-Loop unterstützt. (Auch bei Kernelversionen vor 2.6.) Denn viele Hersteller von Distributionen bauen Crypto-Loop selbständig in ihre Kernel ein. Zur Überprüfung kann der weiter unten beschriebene Weg gegangen werden, um ein verschlüsseltes Dateisystem zu erzeugen.
Sollte wieder Erwarten der Kernel kein Crypto-Loop unterstützen, kann folgender Weg beschritten werden. Es ist dabei Voraussetzung, dass die Kernel-Sourcen des aktuell verwendeten Kernels installiert sind. (Oder des Kernels, welcher neu installiert werden soll) Zusätzlich müssen diese richtig konfiguriert (Plattform, etc.) und übersetzt worden sein. Zuerst ist die Datei loop-AES-latest.tar.bz2 von http://loop-aes.sourceforge.net/ herunterzuladen und mit tar -xvjf loop- AES-latest.tar.bz2 zu entpacken. Danach ist in das entstandene Verzeichnis zu wechseln (cd loop-AES-v3.1c) und make auszuführen. Im Normalfall erkennt make automatisch, wo die Kernel Sourcen liegen.
Der manuellen Installation ist auf jeden Fall die automatische Installation der verwendeten Distribution vorzuziehen. Unter Debian kann der Kernel zum Beispiel folgendermaßen übersetzt werden. Zuerst müssen die Kernel Quellcodes (z.B. kernel-source-2.4.27) installiert werden. Zusätzlich sind die Quellcodes für Cryptoloop zu installieren. (Paket loop-aes-source und loop-aes-ciphers-source. Zweites nur, wenn zusätzliche Algorithmen gewünscht werden.) Zum Schluss sind noch die Tools zum Verwenden des Crypto-Loop-Treibers erforderlich: loop-aes-utils. Es ist natürlich auch möglich, die allerneuesten Kernelquellen von www.kernel.org herunter zu laden. Dabei muss allerdings auf die Namen der Verzeichnisse geachtet werden.
Im folgenden wird davon ausgegangen, dass die
insmod loop max_loop=32
bash12
als Shell (Eingabeinterpreter) verwendet wurde und dass alle Befehle mit
Administrator-Rechten, also z.B. unter dem User root auszuführt werden.
Des weiteren wird davon ausgegangen, dass der Kernel 2.4.27 richtig installiert und konfiguriert ist. Zusätzlich zu diesem Kernel wird CryptoLOOP installiert. Der Kernel an sich wird nicht verändert. Trotzdem ist das Vorhandensein der vollständigen Kernel Quellen erforderlich.
Adaptiert13 von Wenzel (2005).
Der CryptoLoop Driver verwaltet in der Standardeinstellung “nur” acht virtuelle Blockdevices. Dies kann schnell zu wenig sein. Daher empfiehlt es sich, das CryptoLoop Kernel Module (loop.o oder loop.ko bei 2.6er Kerneln) mit dem Parameter max_loop zu laden. Somit können bis zu 256 virtuelle Blockdevices verwendet werden:
Laden des Crypto-Loop Kernel Modules mit 32 virtuellen Blockdevices.
Für jedes virtuelle Blockdevices ist ein Interface zu erstellen. Bei diesem Interface handelt es sich um eine spezielle Datei mit dem Namen /dev/loopX. Die ersten acht sind normalerweise vorhanden. Mit dem folgenden Befehl können Interface-Dateien für 32 virtuelle Blockdevices erstellt werden:
Das Ergebnis dieser Operation sollte folgendes sein:
Bei bedarf können folgende Module nachgeladen werden, um weitere Verschlüsselungsalgorithmen neben AES zu verwenden:
Ein Container ist eine Datei, in welchem sich ein verschlüsseltes Dateisystem befindet.
Um solch einen Container zu erstellen, muss zuerst eine Datei (ein Image) erstellt werden. Es ist zu bedenken, dass es nicht möglich ist, die Größe des Containers nachträglich zu verändern. Um eine Größenänderung zu bewerkstelligen, ist ein neuer Container zu erstellen. Danach sind alle Daten aus dem alten in den neuen Container zu kopieren.
Der folgende Befehl erstellt die Image-Datei, welche das Dateisystem enthalten soll. Die Datei wird mit Nullen (Byte 0x00) aufgefüllt.
dd liest von der Eingabedatei (Input File), welche mit if spezifiziert ist und schreibt die gelesenen Daten nach of (Output File, Ausgabedatei). /dev/zero ist eine spezielle Datei, welche unendlich viele Nullen (Byte 0x00) liefert. Der Container ist hier mit /Container.img benannt. Die Menge der Daten (die Größe des Containers) wird errechnet, indem bs (Block Size) mit count multipliziert wird. In diesem Fall handelt es sich um 25 MByte.
Mit Hilfe eines Hex-Editors kann an dieser Stelle nachgewiesen werden, dass die erstellte Datei tatsächlich nur Nullen enthält. Ein hexdump soll den Hexeditor an dieser Stelle ersetzen.
Glücklicherweise komprimiert hexdump die Ausgabe selbstständig. Das * bedeutet, dass alle folgenden Zeilen mit der Ersten identisch sind. Die erste Nummer jeder Zeile gibt die Position der aktuellen Zeile in der Datei an. Es geht mit 0000000 los und endet mit 1900000. 1900000 ist eine Hexadezimalzahl und ist gleich 26214400 Bytes. Das sind 25 * 1024 * 1024 Bytes, also 25 MByte.
Die Erstellung einer verschlüsselten Partition weicht nicht weit von dieser Beschreibung ab. Statt /Container.img muss die Partition (z.B. /dev/hda5 für die erste logische Partition auf der ersten Festplatte) angegeben werden. Das Erstellen der “Datei” mittels dd entfällt. Sonst kann die hier gegebene Beschreibung angewendet werden. Hinweis: Bei Partitionen ist mit äußerster Vorsicht zu arbeiten, denn der Inhalt der verwendeten Partition wird überschrieben. Daher den Namen des verwendeten Blockdevices immer mehrmals überprüfen.
Der nächste Schritt ist das Verbinden der Datei mit dem virtuellen Blockdevice. Dies wird mit Hilfe von losetup durchgeführt:
Der zu verwendende Verschlüsselungsalgorithmus wird mit -e bekanntgemacht. Bei der ersten übergebenen Datei muss es sich um das virtuelle Blockdevice handeln. Die zweite ist die Datei, die auf das virtuelle Blockdevice gemappt werden soll. Werden die Parameter -e und -C weggelassen, so enthält /dev/loop4 exakt dieselben Daten wie /Container.img, nur mit dem Unterschied, dass /dev/loop4 als Blockdevice gemountet werden kann.
In diesem Fall werden alle Daten, welche nach /dev/loop4 geschrieben werden, mit dem eingegebenen Password14 verschlüsselt und dann nach /Container.img weitergereicht. Der Lesezugriff auf /dev/loop4 funktioniert umgekehrt. Die Daten werden von /Container.img gelesen, entschlüsselt und dann an den lesenden Prozess weitergereicht.
Das Password wird nach der Eingabe gehasht. Dies führt dazu, dass der Schlüsselraum15 optimaler ausgenutzt wird. Denn Zahlen und Buchstaben stellen nur eine kleine Auswahl des Zeichensatzes eines Computers dar. Durch Hashing wird eine Zeichenkette erzeugt, welche alle Zeichen enthalten kann. Diese wird dann als Schlüssel für AES verwendet.
Der Parameter -C n versucht, es möglichen Angreifern etwas schwerer
zu machen. Die Ausgabe der Hash-Funktion wird 1000 * n mal mit
AES25616
verschlüsselt, bevor sie als Schlüssel für die eigentliche Verschlüsselung dient. Bei
Verwendung des Parameters -C 5000 ist eine deutliche Verzögerung zwischen der
Eingabe des Passwortes und der Fertigstellung des Befehls zu beobachten. Wird der
Parameter weggelassen, kann keine nennenswerte Verzögerung festgestellt werden.
Diese Verzögerung ist im Normalfall nicht störend. Versucht jedoch jemand die
Verschlüsselung zu brechen, indem er alle Wörter eines Wörterbuches durchprobiert, so
wird ihm diese Verzögerung zum Verhängnis. Denn sie tritt bei jedem Versuch auf und
lässt die Zeit zum Durchprobierten etwa um den Faktor 1000 * n steigen, was einen
Angriff erheblich erschwert.
root@LBlacky:/ > tune2fs -i 12m -m0 -c 9999 /dev/loop4
tune2fs 1.37 (21-Mar-2005)
Setting maximal mount count to 9999
Setting interval between check 31104000 seconds
Setting reserved blocks percentage to 0 (0 blocks)
Der folgende Befehl gibt den aktuellen Status eines virtuellen Blockdevices aus. Es ist zu erkennen, dass AES zur Verschlüsselung verwendet wird und dass die gemappte Datei /Container.img ist.
Eine kleine Schleife kann auch hier eingesetzt werden, um alle Devices abzufragen.
Der nächste Schritt ist das Erstellen eines Dateisystems in dem Container. In diesem Fall wird ein ext2-Dateisystem erstellt.
Es ist sinnvoll, das so eben erstellte Dateisystem noch etwas feiner abzustimmen. Normalerweise werden 5% des Speicherplatzes auf einem Dateisystem für den User root reserviert, um sicherzustellen, dass alle Systemdienste genug Speicherplatz haben. Hier wird davon ausgegangen, dass keine Systemdienste im Container laufen. Daher werden mit -m0 0% reserviert. Ext2 Dateisysteme werden nach eine einstellbaren Anzahl von Tagen oder von mount-Operationen vollständig getestet. Dies kann nicht abgeschaltet werden, aber es ist möglich, die größten möglichen Werte einzustellen. Test einmal im Jahr (12Monate) -i 12m und aller 9999 mounts -c 9999
Nun ist das Dateisystem erstellt und kann gemountet werden. Dazu wird vorher der mount-point17 erstellt.
Der Container kann jetzt verwendet werden. In diesem Fall wurde repräsentativ eine Datei in den Container kopiert:
Der Beginn dieser Datei wurde dann im Dateisystem gesucht und ausgegeben:
Danach wurde die gleiche Stelle in der gemappten Datei untersucht
 àÔÐåí.[..."|
àÔÐåí.[..."| Es ist zu erkennen, dass die kopierte Datei als Klartext in das Dateisystem, also auf das virtuellem Blockdevice geschrieben wurde. Aufgrund der eingeschalteten Verschlüsselung ist an derselben Stelle in der gemappten Datei nur “Datenschrott” vorzufinden.
Nach Benutzung eines Containers ist es wichtig, diesen wieder zu umounten, da sonst jeder auf die enthaltenen Daten zugreifen kann. Dabei ist es sehr wichtig daran zu denken, das virtuelle Blockdevice wieder freizugeben. Ist dies nicht geschehen, kann ein Angreifer durch Ausführen eines entsprechenden mount-Befehls auf die Daten ohne Eingabe des Passwortes zugreifen.
Der letzte Befehl fragt den Status des virtuellen Blockdevices ab. Dies sollte nach der Freigabe in einer Fehlermeldung resultieren.
Das alles geht auch einfacher. Ist der Container erstellt, so kann er direkt mit mount gemountet werden. In diesem Fall kümmert sich mount automatisch um die Vergabe und Freigabe des virtuellen Blockdevices.
Natürlich ist es an dieser Stelle sehr zu empfehlen, das Passwort zu erinnern. itercountk definiert das gleiche wie bei losetup der Parameter -C und ist selbstverständlich identisch zu wählen. diff vergleicht die beiden übergebenden Dateien. Keine Ausgabe bedeutet, dass beide Dateien identisch sind. Nach diesem Vergleich werden die Zustände alle virtuellen Blockdevices ausgegeben. Mount wählte automatisch das erste freie, hier /dev/loop0. Das Freigeben des Containers geschieht mit umount /crypto. Wie zu erkennen ist, wurde das verwendete virtuelle Blockdevice ebenfalls freigegeben.
Bei dem Verschlüsseln von Daten wird leicht vergessen, dass die verschlüsselten Daten für die Benutzung entschlüsselt werden. Wer eine geheime Datei von einer verschlüsselten Partition in den Editor lädt, kopiert die geheime Datei unverschlüsselt in den Hauptspeicher des Computers. Es ist daher darauf zu achten, dass keine Programme laufen, die den Hauptspeicher auslesen könnten. Des weiteren besteht die Gefahr, dass ein Teil des Hauptspeichers in die Swap-Partition ausgelagert wird. Nun ist ein Teil der geheimen Datei wieder unverschlüsselt auf der Festplatte. Dies kann vermieden werden, indem entweder keine Swap-Partition verwendet wird oder diese ebenfalls verschlüsselt wird. Die Verschlüsselung führt an dieser Stelle natürlich wieder zu Performanceverlust. Das gleiche Problem tritt bei dem Verzeichnis für temporäre Dateien (/tmp) auf. Viele Programme speichern dort Dateien zwischen, was dazu führen kann, dass geheime Dateien aus dem verschlüsselten Container unverschlüsselt auf der Festplatte landen.
Swap-Partition verschlüsseln:
Die folgende Zeile in der Datei /etc/fstab muss erweitert werden:
/dev/hdXX none swap sw 0 0
Erweiterte Zeile:
/dev/hdXX none swap sw,loop=/dev/loopX,encryption=AES128 0 0
Es ist ratsam, die Swap-Partition mit einem Hexeditor zu untersuchen. So kann schnell festgestellt werden, ob diese auch tatsächlich verschlüsselt ist.
Die Sicherheit der verschlüsselten Daten ist immer (nur) so gut wie das Passwort. Ein zu einfaches Passwort kann schnell erraten werden. Ein vergessenes Passwort schützt die Daten sehr effektiv vor dem Eigentümer.
Wer Daten verschlüsselt, sollte sich darüber im klaren sein, dass er womöglich nicht mehr auf seine Daten zugreifen kann, wenn etwas schief gegangen ist. Es sollte daher selbstverständlich sein, immer mindestens zwei Wege zu haben, um seine Daten zu entschlüsseln. Ein einfacher und sehr guter “zweiter Weg” ist die Linux-Live-CD Knoppix18. Von dieser CD kann ein vollständiges Linux mit Crypto-Loop-Unterstützung gebootet werden. Es ist sehr zu empfehlen, den Knoppix-Weg vor einem Systemcrash auszuprobieren. Denn dann ist sofort erkennbar, wenn etwas nicht klappt. (Z.B. Passwort, Algorithmus oder itercountk-Wert falsch). Das Notieren dieser Werte an einem sicheren Ort ist ebenfalls empfehlenswert. Denn nach einem halben Jahr ist der Algorithmus oder itercountk-Wert in Vergessenheit geraten, was zu Problemen führen kann.
Backups zu erstellen ist auch immer eine gute Idee. Wenn überhaupt, sollten Backups erst dann verschlüsselt werden, wenn man schon einige Erfahrung mit Verschlüsselung hat (und wenn der zweite Weg ausprobiert wurde). Auf jeden Fall sollte vor der Erstanwendung einer Verschlüsselung der Datenbestand gesichert werden!
Um einen Überblick über die Performance von AES bzw. von Crypto-Loop zu erhalten, wurde ein Performancevergleich durchgeführt. Dieser Test wurde auf einem Pentium III 850 MHz Computer einmal mit und einmal ohne Verschlüsselung durchgeführt. Es wurden jeweils 250MByte von der Festplatte gelesen.
Die Transferrate wurde mit Hilfe von dd gemessen. Ausgabedatei (of) war /dev/null. Alles was auf dieses spezielle Device geschrieben wird, hört schlicht und einfach auf zu existieren. Es wird nicht weiter verarbeitet.
“Normales” lesen von Festplatte:
Transferrate: ca. 17MByte/s. CPU-Last ca. 27%
Lesen eines verschlüsseltem Bereiches von Festplatte (inklusive entschlüsseln).
Transferrate: ca. 12MByte/s. CPU-Last ca. 64%
Es ist zu erkennen, dass die Entschlüsselung den Datentransfer um gut 35% verlangsamt und fast zweieinhalb mal soviel Rechenlast (CPU-Last) erzeugt.
11MByte/s entspricht 24063 512_Byte_Blöcken/s
Wird nun davon ausgegangen, dass statt der Entschlüsslung jedes 512_Byte_Blockes, immer der selbe Block mit einem anderen Password entschlüsselt wird, würde das Durchprobieren aller möglichen Passwörter ca. 1.5 * 1066 Jahre dauern. In dieser Rechnung ist weder das Analysieren des gewonnenen Klartextblockes (z.B. vergleichen mit einem bekannten Klartextblock) noch das Initialisieren des Verschlüsselungsalgorithmus inbegriffen. Diese Faktoren würden die Zeit noch verlängern.
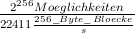 *
* ≈ 1.5 * 1066Jahre
≈ 1.5 * 1066Jahre
Wird davon ausgegangen, dass das Password aus nur einem Wort der englischen Sprache besteht, welches im Oxford Dictionary steht, so beschränkt sich die Anzahl der möglichen Passwörter auf 41480019. Das Durchprobieren aller dieser Möglichkeiten würde mit dem genannten Rechner gerade mal ca. 17 Sekunden dauern.
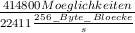 ≈ 17s
≈ 17s
Es sind bei dem Crypto-Loop-Driver allerdings normalerweise nur Passwörter mit 20 oder mehr Zeichen erlaubt. Wird nun angenommen, dass das Password aus fünf Wörtern aus dem englischen Wörterbuch besteht, so ergeben sich 4148005 ≈ 1.2 * 1028 Möglichkeiten. Unter der Annahme, dass die Wörter rein zufällig zusammengesetzt wurden (also keinen Satz bzw. Sinn ergeben müssen) folgt daraus, dass es etwa 1.6 * 1016 Jahre dauern würde, alle Möglichkeiten durchzuprobieren.
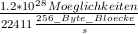 *
*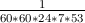 ≈ 1.6 * 1016Jahre
≈ 1.6 * 1016Jahre
Im statistischen Mittel wird es notwendig sein, die Hälfte alle Passwörter durchzuprobieren, um das richtige zu finden. Das bedeutet, dass im statistischen Mittel nur die Hälfte der errechneten Zeit notwendig ist, um das Passwort zu finden.
Durch das Aktivieren der weiter oben genannten Option -C bei losetup bzw. itercountk bei mount kann diese Form der Attacken erheblich erschwert werden. Denn das Initialisieren des Verschlüsselungsverfahrens wird erheblich aufwendiger und langwieriger durch Einsatz dieses Parameters.
Corbet et al (2004) A weak cryptoloop implementation in Linux?
[Online] Available at http://lwn.net/Articles/67216/ (accessed 22. December)
Daemen, J.; Rijmen, V. (2002) The Design of Rijndael. Berlin Heidelberg: Springer-Verlag. ISBN 3-540-42580-2.
Deters, D. (2002) Systematisierung der symmetrischen kryptographischen Verfahren
[Online] Available at
http://www.informatik.hu-berlin.de/Forschung_Lehre/algorithmenII/
Lehre/SS2002/Ana_krypt_Alg/02Systematisierung/Systematisierung.html
(accessed 20. December 2005)
Hölzer, R. (2004) Cryptoloop HOWTO. [Online] Available at
http://www.tldp.org/HOWTO/Cryptoloop-HOWTO/ (accessed 22. December
2005)
Ruusu, J (2004) “README” von Loop-AES. [Online] Available at
http://loop-aes.sourceforge.net/loop-AES.README
van Rees, J (2005) Introduction to Cryptography and Cryptosystems: Assignments
[Online] Available at
http://www.cs.umanitoba.ca/~cs414/assignments/(test2output.txt)
(accessed 26. December 2005)
Wenzel, R. (2005) Verschluesselte Dateisysteme und Container.
[Online] Available at
http://www.ruwela.de/Linux-Befehls-Beispiele/node16.html (accessed 22.
December 2005)
Wilkin, C (2004) Der Algorithmus des “Advanced Encryption Standard”.
[Online] Available at http://www.ainformatik.fh-trier.de/~scheerhorn/
(accessed 20. December 2005)
|
Pages by Andreas Hofmeier |
 |
 Impressum/Note Datenschutzerklärung Impressum/Note Datenschutzerklärung |
|---|
|
http[s]://www.abmh.de/fhs/crypt/AES2LoopAES/RST_AES.HTML/index.html |
|---|
 |
(c) Andreas B. M. Hofmeier This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 Germany License |