
 Impressum/Note Datenschutzerklärung
Impressum/Note Datenschutzerklärung|
Pages by Andreas Hofmeier |
 |
 Impressum/Note Datenschutzerklärung Impressum/Note Datenschutzerklärung |
|---|
|
http[s]://www.abmh.de/einstein/relativ/index.html |
|---|
Inhalt:
Die Relativitätstheorien sind nicht etwa deshalb als unverständlich bekannt, weil sie schwer nachzuvollziehen wären, sondern eher deshalb, weil man ihre Folgerungen nur schwer glauben kann! Das liegt daran, daß wir alles an unseren bisherigen Erfahrungen messen, die jedoch nur einen kleinen Teil einer Gesamtheit ausmachen (dem Universum, oder noch mehr?). Daher kommt man kaum auf die Idee, unsere Erfahrungen könnten nur ein Spezialfall von viel allgemeiner gefaßten Gesetzlichkeiten sein.
 Albert Einstein wurde am 14.03.1879, in Ulm geboren und starb
am 18.04.1955 in Princeton, NJ. Er verbringt seine Jugend in
München, wo seine Familie einen Elektrofachbetrieb besitzt. In
seinen jungen Jahren gibt es keine äußerlichen Zeichen für die
Genialität, die Einstein schon damals besitzt. Er beginnt erst
im Alter von drei Jahren zu sprechen und kann sich mit neun
Jahren noch nicht fließend unterhalten. Aber trotz alle
dem entwickelt er eine brillante Neugier für die Natur und
komplexe mathematische Konzepte. Im Alter von zwölf Jahren z.B.
bringt er sich die euklidische Geometrie bei. Einstein haßt die
stumpfen und phantasielosen Methoden der Münchener Schulen, die
wir ja nur allzugut aus Filmen und Geschichten kennen. Als ein
erneuter Fehlschlag des Geschäfts, die Familie nach
Mailand führt, nutzt der damals 15 Jährige Albert die
Gelegenheit von der Schule zu gehen und ein Jahr mit seinen
Eltern zu verbringen. Als sich dann aber die Frage stellt, was
Albert einmal werden soll, entscheidet er sich, das Gymnasium in
Aarau (Schweiz) zu besuchen und absolviert die Polytechnik in
Zürich. Auch hier gefallen ihm die Methoden der Lehrer ganz und
gar nicht. Er schwänzt häufig Kurse und nutzt die Zeit, um
privat Physik zu studieren oder spielt auf seiner geliebten
Violine, auf der er im Alter von 6 Jahren beginnt zu spielen. Er
besteht alle Examen und graduiert von der Polytechnik in 1900
durch das Benutzen der Hefte eines Klassenkameraden. Seine
Professoren meinen damals, daß er auf keinen Fall für eine
Position an der Universität in Frage kommen würde. Für zwei
Jahre arbeitet Einstein als Tutor und Vertretungslehrer in der
Schweiz. Im Jahre 1902 sichert er sich dann eine Stellung am
Schweizer Patentamt in Bern. Doch was macht ihn so besonders und
woher kommt seine Genialität. Er selbst schreibt in seiner
Auto-Biographie, daß es wahrscheinlich seine Mutter war, die ihn
so inspirierte und ihr Einfluß der Einstein so anders als alle
anderen Wissenschaftler werden ließ. Seine Mutter Pauline wird
1858 in Cannstadt geboren und stirbt 1920 in Berlin. Sie und ihr
Ehemann Hermann (geboren 1847 in Buchau, gestorben 1902 in
Mailand ) ziehen ein Kind groß, das so wichtig für die Welt
sein sollte, wie wir nachher sehen werden. Die beste Beziehung
hat Albert zu seiner Schwester Maja (*1881,gestorben1949),
dessen Tod ihn weitaus mehr schockiert als der seiner beiden
Ehefrauen. Am 6. Januar 1903 heiratet Einstein seine
langjährige Klassenkameradin aus der Polytechnik, Mileva
Maric. Sie haben zusammen zwei Söhne Hans-Albert und Eduard von
denen letzteren eine schwere psychische Krankheit ereilte.
Diese Ehe hält auch nicht sehr lange und so kommt es, daß
Einstein einige Jahre später seine Cousine Elsa Koch
heiratet. Im Jahre 1905 erhält er den Doktortitel der Uni Zürich
für seine Theorie der molekularen Dimensionen. Er
veröffentlicht außerdem seine drei bekanntesten Theorien , die
die Physik des 20. Jahrhunderts zu dem gemacht haben, was es
jetzt ist. Auf diese und andere werde ich später
zurückkommen. Das Leben Einsteins wird schlagartig besser und er
ist weltweit die gefragteste Persönlichkeit schlechthin. In 1922
bekommt er dann u.a. für den Photoelektrischen Effekt den
Nobelpreis für Physik. Da Einstein jüdisch ist und die
Entwicklung des Zionismus vorantreibt und kräftig unterstützt,
muß er in den 30- Jahren nach Amerika auswandern und wird
Professor für Physik an der Universität in Princeton,NJ. Während
des 1.Weltkrieges hilft er, durch seine Entdeckungen im Bereich
der Nuklearphysik indirekt, mit etlichen anderen
Wissenschaftlern, die erste Atombombe zu entwickeln und rettet
somit laut der US Regierung tausende von Marines, die (ohne die
Kapitulation der Japaner nach Hiroshima und Nagasaki) beim
anlanden an der südlichen Küste Japans den sicheren Tod gefunden
hätten. Obwohl Einstein eigentlich nichts mit dem Bombenabwurf
zu tun hat und auch nichts über ihn weiß plagt es ihn
sein restliches Leben lang, daß er zu der Erfindung dieser
schrecklichen Waffe beigetragen hatte. Nach dem zweiten
Weltkrieg wird ihm angeboten Präsident von Israel zu werden. Er
lehnt allerdings, dankend, ab und verschreibt sich den Rest
seines Lebens Frieden zu schaffen und die Abrüstung
voranzutreiben . Er schreibt seine Autobiographie, die zum
größten Teil aus seiner Kindheit und Jugend erzählt. Er wird zum
Symbol des Zionismus und zum Denker des Jahrhunderts, in dem er
sehr ausführlich seine Philosophie über "Gott und die Welt" in
etlichen Büchern offenbart.
Albert Einstein wurde am 14.03.1879, in Ulm geboren und starb
am 18.04.1955 in Princeton, NJ. Er verbringt seine Jugend in
München, wo seine Familie einen Elektrofachbetrieb besitzt. In
seinen jungen Jahren gibt es keine äußerlichen Zeichen für die
Genialität, die Einstein schon damals besitzt. Er beginnt erst
im Alter von drei Jahren zu sprechen und kann sich mit neun
Jahren noch nicht fließend unterhalten. Aber trotz alle
dem entwickelt er eine brillante Neugier für die Natur und
komplexe mathematische Konzepte. Im Alter von zwölf Jahren z.B.
bringt er sich die euklidische Geometrie bei. Einstein haßt die
stumpfen und phantasielosen Methoden der Münchener Schulen, die
wir ja nur allzugut aus Filmen und Geschichten kennen. Als ein
erneuter Fehlschlag des Geschäfts, die Familie nach
Mailand führt, nutzt der damals 15 Jährige Albert die
Gelegenheit von der Schule zu gehen und ein Jahr mit seinen
Eltern zu verbringen. Als sich dann aber die Frage stellt, was
Albert einmal werden soll, entscheidet er sich, das Gymnasium in
Aarau (Schweiz) zu besuchen und absolviert die Polytechnik in
Zürich. Auch hier gefallen ihm die Methoden der Lehrer ganz und
gar nicht. Er schwänzt häufig Kurse und nutzt die Zeit, um
privat Physik zu studieren oder spielt auf seiner geliebten
Violine, auf der er im Alter von 6 Jahren beginnt zu spielen. Er
besteht alle Examen und graduiert von der Polytechnik in 1900
durch das Benutzen der Hefte eines Klassenkameraden. Seine
Professoren meinen damals, daß er auf keinen Fall für eine
Position an der Universität in Frage kommen würde. Für zwei
Jahre arbeitet Einstein als Tutor und Vertretungslehrer in der
Schweiz. Im Jahre 1902 sichert er sich dann eine Stellung am
Schweizer Patentamt in Bern. Doch was macht ihn so besonders und
woher kommt seine Genialität. Er selbst schreibt in seiner
Auto-Biographie, daß es wahrscheinlich seine Mutter war, die ihn
so inspirierte und ihr Einfluß der Einstein so anders als alle
anderen Wissenschaftler werden ließ. Seine Mutter Pauline wird
1858 in Cannstadt geboren und stirbt 1920 in Berlin. Sie und ihr
Ehemann Hermann (geboren 1847 in Buchau, gestorben 1902 in
Mailand ) ziehen ein Kind groß, das so wichtig für die Welt
sein sollte, wie wir nachher sehen werden. Die beste Beziehung
hat Albert zu seiner Schwester Maja (*1881,gestorben1949),
dessen Tod ihn weitaus mehr schockiert als der seiner beiden
Ehefrauen. Am 6. Januar 1903 heiratet Einstein seine
langjährige Klassenkameradin aus der Polytechnik, Mileva
Maric. Sie haben zusammen zwei Söhne Hans-Albert und Eduard von
denen letzteren eine schwere psychische Krankheit ereilte.
Diese Ehe hält auch nicht sehr lange und so kommt es, daß
Einstein einige Jahre später seine Cousine Elsa Koch
heiratet. Im Jahre 1905 erhält er den Doktortitel der Uni Zürich
für seine Theorie der molekularen Dimensionen. Er
veröffentlicht außerdem seine drei bekanntesten Theorien , die
die Physik des 20. Jahrhunderts zu dem gemacht haben, was es
jetzt ist. Auf diese und andere werde ich später
zurückkommen. Das Leben Einsteins wird schlagartig besser und er
ist weltweit die gefragteste Persönlichkeit schlechthin. In 1922
bekommt er dann u.a. für den Photoelektrischen Effekt den
Nobelpreis für Physik. Da Einstein jüdisch ist und die
Entwicklung des Zionismus vorantreibt und kräftig unterstützt,
muß er in den 30- Jahren nach Amerika auswandern und wird
Professor für Physik an der Universität in Princeton,NJ. Während
des 1.Weltkrieges hilft er, durch seine Entdeckungen im Bereich
der Nuklearphysik indirekt, mit etlichen anderen
Wissenschaftlern, die erste Atombombe zu entwickeln und rettet
somit laut der US Regierung tausende von Marines, die (ohne die
Kapitulation der Japaner nach Hiroshima und Nagasaki) beim
anlanden an der südlichen Küste Japans den sicheren Tod gefunden
hätten. Obwohl Einstein eigentlich nichts mit dem Bombenabwurf
zu tun hat und auch nichts über ihn weiß plagt es ihn
sein restliches Leben lang, daß er zu der Erfindung dieser
schrecklichen Waffe beigetragen hatte. Nach dem zweiten
Weltkrieg wird ihm angeboten Präsident von Israel zu werden. Er
lehnt allerdings, dankend, ab und verschreibt sich den Rest
seines Lebens Frieden zu schaffen und die Abrüstung
voranzutreiben . Er schreibt seine Autobiographie, die zum
größten Teil aus seiner Kindheit und Jugend erzählt. Er wird zum
Symbol des Zionismus und zum Denker des Jahrhunderts, in dem er
sehr ausführlich seine Philosophie über "Gott und die Welt" in
etlichen Büchern offenbart.
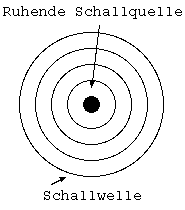 Normalerweise breiten sich Schallwellen in kugelförmigen Bahnen
um ihre Schallquelle aus. Zur Vereinfachung betrachten wir nur
einen zweidimensionalen Raum. Was passiert aber, wenn sich die
Schallquelle bewegt? Die Schallwellen werden vor der
Schallquelle gestaucht (also zusammengedrückt) und hinter der
Schallquelle gedehnt (also auseinandergezogen).
Normalerweise breiten sich Schallwellen in kugelförmigen Bahnen
um ihre Schallquelle aus. Zur Vereinfachung betrachten wir nur
einen zweidimensionalen Raum. Was passiert aber, wenn sich die
Schallquelle bewegt? Die Schallwellen werden vor der
Schallquelle gestaucht (also zusammengedrückt) und hinter der
Schallquelle gedehnt (also auseinandergezogen).
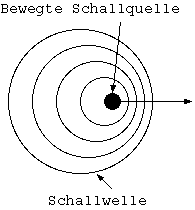 Warum?
Warum?
Schall ist eine Verdichtung bzw. eine Entdichtung der
Luft. Da der Vorgang des ver/-entdichten einige Zeit in Anspruch
nimmt, braucht der Schall eine gewisse Zeit um von A nach B zu
kommen. Diese Zeit ist abhängig vom Medium. Der Schall setzt
sich nun mit einer konstanten Geschwindigkeit fort, der
Schallgeschwindigkeit, welche vom Medium in dem er sich bewegt
abhängig ist. Wenn sich die Schallquelle bewegt, ändert sich die
Schallgeschwindigkeit nicht, da die Schallgeschwindigkeit
relativ (abhängig) zum Medium ist. Das Medium, die Luft, steht
still. Die Frequenz (die Höhe des Tones, den wir hören) ist nun
zu definieren mit Impulse (Verdichtungen) pro Zeit
(Sekunden). Bewegt sich nun die Schallquelle, so bewegen sich
die Schallwellen ``nur'' mit Schallgeschwindigkeit und nicht mit
Schallgeschwindigkeit + Geschwindigkeit der Schallquelle von
dieser weg. Das führt dazu, das der Schall nicht schnell genug
weg kommt. Der nächste Impuls kommt bevor der vorherige Impuls
weit genug weg ist. Das führt dazu, das die Frequenz vor der
Schallquelle zunimmt, und hinter der Schallquelle
abnimmt. Diesen Effekt kann man im Alltag beobachten, wenn ein
Auto an einem vorbei fährt. Zuerst hören wir einen hohen Ton,
wenn das Auto auf uns zu fährt, dann einen niedrigeren Ton, wenn
das Auto an uns vorbei ist und sich entfernt. (Die Lautstärke
mal außer acht gelassen, sie nimmt mit der Entfernung
Quadratisch ab.) Man kann den Schall ja sogar überholen. Die
Flugzeuge machen das vor. Diese fliegen mit
Überschallgeschwindigkeit, aus diesem Grund hört man die von den
Motoren der Flugzeuge ausgehenden Schallwellen nicht. Der Rest
an Geräuschen wandert über das Flugzeug direkt.
Was ist Bewegung überhaupt? Wir definieren Bewegung mit überwundener Strecke pro Zeit.
Was passiert mit dem Schall, wenn er sich in einem sich
gleichförmig bewegendem geschlossenem Raum befindet?
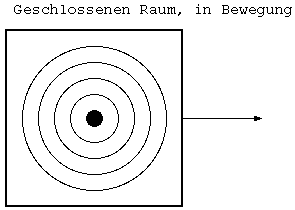 Da sich das Medium (die
Luft), durch das der Schall wandert, in dem Raum ist und sich
genauso bewegt, ist die Schallgeschwindigkeit relativ zu einem
stehendem Beobachter außerhab des Raumes größer, da sich der
Schall ja mit Schallgeschwindigkeit durch den Raum bewegt und
der Raum sich auch noch mit einer gewissen Geschwindigkeit
bewegt. Dies gilt natürlich nur wenn der Schall und der Raum
sich in die gleiche Richtung bewegen. Ist die Richtung
entgegengesetzt, ist die Schallgeschwindigkeit kleiner. Die
Schallgeschwindigkeit für den externen Beobachter ist also
Schallgeschwindigkeit plus Geschwindigkeit des Raums!
Da sich das Medium (die
Luft), durch das der Schall wandert, in dem Raum ist und sich
genauso bewegt, ist die Schallgeschwindigkeit relativ zu einem
stehendem Beobachter außerhab des Raumes größer, da sich der
Schall ja mit Schallgeschwindigkeit durch den Raum bewegt und
der Raum sich auch noch mit einer gewissen Geschwindigkeit
bewegt. Dies gilt natürlich nur wenn der Schall und der Raum
sich in die gleiche Richtung bewegen. Ist die Richtung
entgegengesetzt, ist die Schallgeschwindigkeit kleiner. Die
Schallgeschwindigkeit für den externen Beobachter ist also
Schallgeschwindigkeit plus Geschwindigkeit des Raums!
Wie kann man überhaupt feststellen, ob sich der Raum, in dem man sich befindet gleichförmig bewegt? Natürlich, man kann aus dem Fenster sehen, aber was wenn der Raum keine Fenster hat? Kann man feststellen, ob sich der Raum gleichförmig bewegt, ohne sich auf andere außerhalb des Raumes befindliche Punkte Bezug zu nehmen? NEIN!
Nehmen wir mal an, in diesem Raum steht ein Lampe. Bewegt diese Lampe sich? Also relativ zu einer in dem Raum befindlichen Beobachter nicht. Aber für ein Außerhalt des Raumes stehenden Beobachter würde sich die Lampe bewegen. Nun ist natürlich die Frage zu stellen, ob der Beobachter außerhalb des Raumes wirklich steht. Denn man kann ja nicht feststellen, ob man sich bewegt.
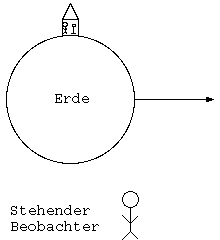 Um ein bischen Bezug zur Realität zu bekommen, stellen wir den
Raum mal auf die Erde. Bewegt sich die Lampe nun? Für jemanden,
der auf der Erde steht nicht. Nun dreht sich die Erde aber um
ihre eigene Achse, insgesamt aber um die Sonne, unser
Sonnensystem bewegt sich innerhalb der Galaxie und der
Milchstraße etc. Man kann folglich immer nur sagen, daß sich ein
Objekt mit einer bestimmten Geschwindigkeit und
Bewegungsrichtung relativ zu diesem oder jenem Bezugspunkt
bewegt!
Um ein bischen Bezug zur Realität zu bekommen, stellen wir den
Raum mal auf die Erde. Bewegt sich die Lampe nun? Für jemanden,
der auf der Erde steht nicht. Nun dreht sich die Erde aber um
ihre eigene Achse, insgesamt aber um die Sonne, unser
Sonnensystem bewegt sich innerhalb der Galaxie und der
Milchstraße etc. Man kann folglich immer nur sagen, daß sich ein
Objekt mit einer bestimmten Geschwindigkeit und
Bewegungsrichtung relativ zu diesem oder jenem Bezugspunkt
bewegt!
Die Frage ``Was ist Licht?'', ist bis Heute noch nicht genau geklärt. Um gewisse Eigenschaften des Lichtes zu erklären muß man annehmen das es sich um eine Welle und/oder ein Teilchen handelt. Wir gehen hier davon aus, das Licht zu den elektromagnetischen Wellen gehört. Wie zum Beispiel Radiowellen, UV-Strahlen, Infrarote-Strahlen. (Obwohl das wissen wir auch noch nicht so genau)
Das Licht bewegt sich mit einer Geschwindigkeit von ca. 300.000 km/s durch das Vakuum. Aber Halt, durch welches Medium bewegt sich das Licht denn dann? Im Vakuum ist nichts. Schall könnte sich in einem Vakuum nicht ausbreiten, da es dort kein Medium gibt. Es gibt im Vakuum kein Schall! Wie kann sich Licht ausbreiten? Man nannte das des Medium Lichtes Äther. Dieser Äther müßte demnach überall vorhanden sein. Im Vakuum genauso wie in Materie. Die Sache hat nur einen Haken, wenn es Äther gäbe, währe dieser Absolut still, somit könnte man absolute Bewegung feststellen, dies ist aber nicht möglich. Mit dem Michelson-Morleysche Versuch wurde endgültig bewiesen, das es kein Äther gibt.
Nur wenn das Licht kein Medium hat/braucht, wozu ist die Ausbreitung des Lichtes dann Relativ? Zu nichts, die Lichtgeschwindigkeit ist eine Naturkonstante und ist für jeden Beobachter gleich.
Aber wenn die Lichtgeschwindigkeit für jeden Beobachter gleich
ist, dann muß sich ja was anderes ändern!
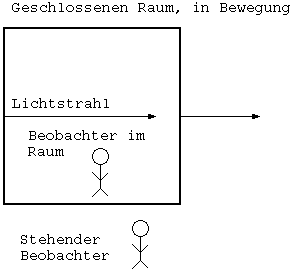 Wenn in einem sich gleichförmig bewegenden Raumes ein
Lichtstrahl von A nach B wandert, mißt man im Raum die
Lichtgeschwindigkeit. Ein außerhalb stehender Beobachter mißt
allerdings auch die Lichtgeschwindigkeit! Wir erinnern uns, die
Schallgeschwindigkeit war für einen externen Beobachter
anders. Wie ist das möglich? Die Lichtgeschwindigkeit ist eine
Konstante und ist für alle Beobachter gleich?
Wenn in einem sich gleichförmig bewegenden Raumes ein
Lichtstrahl von A nach B wandert, mißt man im Raum die
Lichtgeschwindigkeit. Ein außerhalb stehender Beobachter mißt
allerdings auch die Lichtgeschwindigkeit! Wir erinnern uns, die
Schallgeschwindigkeit war für einen externen Beobachter
anders. Wie ist das möglich? Die Lichtgeschwindigkeit ist eine
Konstante und ist für alle Beobachter gleich?
Wir leben in einem Vierdimensionalem Raum-Zeit-Kontinuum. Wir
haben drei Raum Dimensionen (Höhe, Breite und Tiefe) und eine
Zeitdimension (die Zeit).
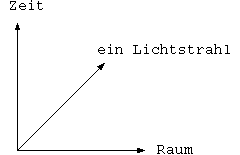 Zur Vereinfachung betrachten wir nur eine Raum und eine
Zeitdimension. Ein Lichtstahl währe unter diesen voraussetzungen
in einem normalen Diagramm also die Winkelhalbierende.
Zur Vereinfachung betrachten wir nur eine Raum und eine
Zeitdimension. Ein Lichtstahl währe unter diesen voraussetzungen
in einem normalen Diagramm also die Winkelhalbierende.
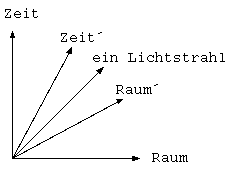 Wenn die Lichtgeschwindigkeit gleich bleibt, dann muß sich
irgend etwas anderes ändern. Aber was bleibt? Nur der Raum und
die Zeit. Da eine Geschwindigkeit Weg (Raum) pro Zeit definiert,
müssen sich beide Werte ändern um die Lichtgeschwindigkeit
konstant zu halten.
Wenn die Lichtgeschwindigkeit gleich bleibt, dann muß sich
irgend etwas anderes ändern. Aber was bleibt? Nur der Raum und
die Zeit. Da eine Geschwindigkeit Weg (Raum) pro Zeit definiert,
müssen sich beide Werte ändern um die Lichtgeschwindigkeit
konstant zu halten.
Das muß man sich erst einmal verinnerlichen, die Zeit und der Abstand sind nicht immer und überall gleich!
Was bedeutet dies?
Wenn man in einem Auto sitzt welches
fährt, muß man dort die exakte Lichtgeschwindigkeit messen,
genauso wie außerhalb. Wie oben beschrieben, muß sich die Zeit
im Auto verlangsamen. Desweiteren muß das Auto in
Bewegungsrichtung kürzer werden. Dies führt dazu, das Weg pro
Zeit der Lichtgeschwindigkeit gleich dem Stehendem Beobachter
sind. Die Zeit bzw. die Längenänderung würde Natürlich nur ein
ausenstehender Beobachter bemerken. Die im Auto sitzenden
Personen könnten die Längen- bzw. Zeitverkürzung nicht messen,
da die Änderungen relativ sind und die relative Geschwindigkeit
zu sich selbst immer null ist. Einfacher ausgedrückt, würde
einer ein Lineal ans fahrende Auto anlegen, würde sich diese
ebenfalls verkürzen, das für dazu, das man die gewohnte Länge
mißt. Formel für Längenverkürzung eines Objektes: ![L' = L * Wurzel aus [ 1 - (v^2 / c^2) ]](fl.gif) . Formel für Zeitverkürzung eines Objektes:
. Formel für Zeitverkürzung eines Objektes: ![t' = t * Wurzel aus [ 1 - (v^2 / c^2) ]](ft.gif) . Wer sich die Formeln ansieht, sieht, das
erwähnenswerte Änderungen erst enstehen, wenn man sich der
Lichtgeschwindigkeit nähert. Was wir selbst mit Flugzeugen
(mehrfache Schallgeschwindigkeit) nicht schaffen. Wir erinnern
uns, das Licht breitet sich mit ca. 300.000 km/s aus, Schall nur
mit 330 m/s. Also ist Schall etwas um das 900.000 langsamer als
das Licht. Also sind wir noch weit von der Lichtgeschwindigkeit,
und somit von nennenswerten Änderungen der Raumzeit,
entfernt. Weiterhin kann die Lichtgeschwindigkeit nicht
überschritten werden, da sonst eine negative Wert unter der
Wurzel entstehen würde, dies ist mathematisch nicht erlaubt.
. Wer sich die Formeln ansieht, sieht, das
erwähnenswerte Änderungen erst enstehen, wenn man sich der
Lichtgeschwindigkeit nähert. Was wir selbst mit Flugzeugen
(mehrfache Schallgeschwindigkeit) nicht schaffen. Wir erinnern
uns, das Licht breitet sich mit ca. 300.000 km/s aus, Schall nur
mit 330 m/s. Also ist Schall etwas um das 900.000 langsamer als
das Licht. Also sind wir noch weit von der Lichtgeschwindigkeit,
und somit von nennenswerten Änderungen der Raumzeit,
entfernt. Weiterhin kann die Lichtgeschwindigkeit nicht
überschritten werden, da sonst eine negative Wert unter der
Wurzel entstehen würde, dies ist mathematisch nicht erlaubt.
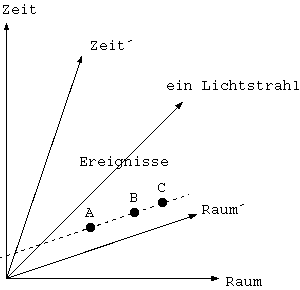 Interessant wird es, wenn man sich die Verschiebung von Raum und
Zeit näher ansieht. Wir haben zwei Beobachter: Den Ersten, der
im Zeit-Raum Aufhält und der Zweite der wegen seiner
Geschwindigkeit in der Raum'-Zeit' aufhält. Für den Ersten
Beobachter geschehen die Ereignisse A, B und C
nacheinander. Alle drei Ereignisse liegen auf einer gedachten
Linie, welche Parallel zu der Raum'-Achse ist. Somit liegen alle
drei Punkte auf dem selben Punkt auf der Zeit'-Achse (sind also
für Zeit' gleichzeitig), aber an unterschiedliche Punkten auf
der Zeit-Achse.
Interessant wird es, wenn man sich die Verschiebung von Raum und
Zeit näher ansieht. Wir haben zwei Beobachter: Den Ersten, der
im Zeit-Raum Aufhält und der Zweite der wegen seiner
Geschwindigkeit in der Raum'-Zeit' aufhält. Für den Ersten
Beobachter geschehen die Ereignisse A, B und C
nacheinander. Alle drei Ereignisse liegen auf einer gedachten
Linie, welche Parallel zu der Raum'-Achse ist. Somit liegen alle
drei Punkte auf dem selben Punkt auf der Zeit'-Achse (sind also
für Zeit' gleichzeitig), aber an unterschiedliche Punkten auf
der Zeit-Achse.
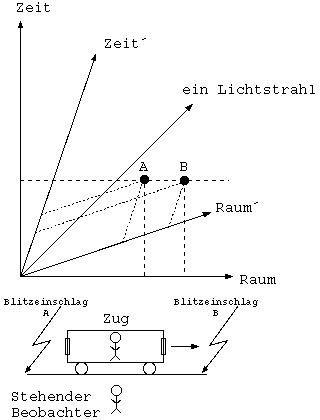 Dies kann man sich mal veranschaulichen, indem man sich einen
fahrenden Zug vorstellt. In der Mitte eines Waagongs steht ein
Beobachter. Und ein weiterer Beobachter steht neben den
Gleisen. Nun beobachtet der neben den Schienen stehende
Beobachter das gleichzeitige einschlagen zweier Blitze. Einer
vor, der andere hinter dem Zug. Der Beobachter ist genau in der
Mitte der Strecke zwischen den beider Einschlägen. Was
Beobachtet nun ein im Zug mitfahrender Beobachter? Gehen wir mal
davon aus, das beide Beobachter auf gleicher Höhe sind, während
die Blitze einschlagen. Tragen wir die Ereignisse in ein
Diagramm ein, so können wir ablesen, das für den im Zug
mitfahrenden Beobachter der Blitz vor dem Zug früher einschlägt
als der Blitz hinter diesem. Sehen wir uns das Diagramm genauer
an: Für den stehenden Beobachter passieren die beiden
Blitzeinschläge gleichzeitig, aber an verschiedenen
Orten. Deshalb müssen die Beiden Punkte, welche die
Blitzeinschläge (Ereignisse) darstellen, auf einer gedachten
Linie, welche Parallel zur Raum-Achse verläuft, liegen. Da die
Ereignisse so auf der gleiche Höhe der Zeit-Achse liegen,
geschehen sie gleichzeitig. Um sich den Zusammenhang des
fahrenden Zuges besser vorstellen zu können, nehmen wir an, das
die Raum-Achse die Gleise ist, auf dem der Zug fährt. Der Zug
fährt vom Koordinatennullpunkt (links) weg also nach
rechts. Ziehen wir nun Linien für das Raum'-Zeit'-Diagramm: Die
Linien, welche zur Zeit'-Achse gehen müssen parallel zur
Raum'-Achse sein und umgekehrt. Haben wir die vier Linien
gezogen, so sehen wir, das die Linien von den Punkten zu der
Zeit'-Achse an verschiedenen Punkten ankommen, also für
Raum'-Zeit'-Diagramm nicht gleichzeitig sind. Der Blitzeinschlag
vor dem Zug, ist früher, da seine Linie weiter unten auf die
Zeit'-Achse trifft als die Linie des Blitzeinschlages hinter dem
Zug.
Dies kann man sich mal veranschaulichen, indem man sich einen
fahrenden Zug vorstellt. In der Mitte eines Waagongs steht ein
Beobachter. Und ein weiterer Beobachter steht neben den
Gleisen. Nun beobachtet der neben den Schienen stehende
Beobachter das gleichzeitige einschlagen zweier Blitze. Einer
vor, der andere hinter dem Zug. Der Beobachter ist genau in der
Mitte der Strecke zwischen den beider Einschlägen. Was
Beobachtet nun ein im Zug mitfahrender Beobachter? Gehen wir mal
davon aus, das beide Beobachter auf gleicher Höhe sind, während
die Blitze einschlagen. Tragen wir die Ereignisse in ein
Diagramm ein, so können wir ablesen, das für den im Zug
mitfahrenden Beobachter der Blitz vor dem Zug früher einschlägt
als der Blitz hinter diesem. Sehen wir uns das Diagramm genauer
an: Für den stehenden Beobachter passieren die beiden
Blitzeinschläge gleichzeitig, aber an verschiedenen
Orten. Deshalb müssen die Beiden Punkte, welche die
Blitzeinschläge (Ereignisse) darstellen, auf einer gedachten
Linie, welche Parallel zur Raum-Achse verläuft, liegen. Da die
Ereignisse so auf der gleiche Höhe der Zeit-Achse liegen,
geschehen sie gleichzeitig. Um sich den Zusammenhang des
fahrenden Zuges besser vorstellen zu können, nehmen wir an, das
die Raum-Achse die Gleise ist, auf dem der Zug fährt. Der Zug
fährt vom Koordinatennullpunkt (links) weg also nach
rechts. Ziehen wir nun Linien für das Raum'-Zeit'-Diagramm: Die
Linien, welche zur Zeit'-Achse gehen müssen parallel zur
Raum'-Achse sein und umgekehrt. Haben wir die vier Linien
gezogen, so sehen wir, das die Linien von den Punkten zu der
Zeit'-Achse an verschiedenen Punkten ankommen, also für
Raum'-Zeit'-Diagramm nicht gleichzeitig sind. Der Blitzeinschlag
vor dem Zug, ist früher, da seine Linie weiter unten auf die
Zeit'-Achse trifft als die Linie des Blitzeinschlages hinter dem
Zug.
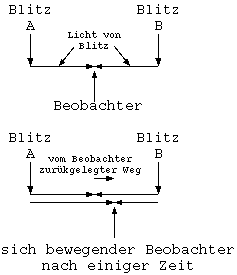 Kommen wir nun von der Abstrakten betrachtung eines Diagrammes
zur Realität: Da die Lichtgeschwindigkeit immer gleich ist,
braucht das Licht, welches von den beider Blitzeinschlägen
ausgeht, exakt die gleiche Zeit um zu der Mitte zu
gelangen. Nochmal etwas einfacher: Zwischen den beiden
Blitzeinschlägen ist ein gewisser Abstand. Der Beobachter steht
genau in der Mitte. Was aber, wenn sich der Beobachter bewegt?
Da das Licht einige Zeit (lassen wir das Maß mal weg) braucht,
um die Mitte zu erreichen, hat der Beobachter die Mitte schon
wieder verlassen. Also braucht das Licht von dem Blitzeinschlag
vor dem sich bewegendem Beobachter weniger Zeit ( = hat kürzeren
Weg) um diesen zu Erreichen als das Licht von dem Blitz hinter
diesem. Für den im Zug mitfahrenden Beobachter schlägt der Blitz
vor dem Zug früher ein.
Kommen wir nun von der Abstrakten betrachtung eines Diagrammes
zur Realität: Da die Lichtgeschwindigkeit immer gleich ist,
braucht das Licht, welches von den beider Blitzeinschlägen
ausgeht, exakt die gleiche Zeit um zu der Mitte zu
gelangen. Nochmal etwas einfacher: Zwischen den beiden
Blitzeinschlägen ist ein gewisser Abstand. Der Beobachter steht
genau in der Mitte. Was aber, wenn sich der Beobachter bewegt?
Da das Licht einige Zeit (lassen wir das Maß mal weg) braucht,
um die Mitte zu erreichen, hat der Beobachter die Mitte schon
wieder verlassen. Also braucht das Licht von dem Blitzeinschlag
vor dem sich bewegendem Beobachter weniger Zeit ( = hat kürzeren
Weg) um diesen zu Erreichen als das Licht von dem Blitz hinter
diesem. Für den im Zug mitfahrenden Beobachter schlägt der Blitz
vor dem Zug früher ein.
Natürlich, bei auf der Erde üblichen
Geschwindigkeiten, ist diese Zeitverschiebung so gering, das sie
ein Mensch nicht erfassen könnte. Des weiteren, können wir nicht
in zwei Richtungen sehen, aber trotzdem interessante
Vorstellung...
Normalerweise sagt man, das man zwei Geschwindigkeiten durch
einfach Addition, Addieren kann. Also v = v1 + v2. Ein
praktisches Beispiel ist eine Modelleisenbahn in einer
Straßenbahn. Fahrt die Starßenbahn mit 20km/h und die
Modelleisenbahn mit 5km/h (relativ zur Straßenbahn) ist dann die
Modelleisenbahn 25km/h schnell? Nein!
Berücksichtigt man die
spezielle Relativitätstheorie, so kommt man auf 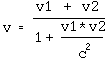 . v = v1 + v2 ist also nur eine Näherungsformel. Für
geringe Geschwindigkeiten (wie sie auf der Erde üblich sind)
liefert sie jedoch ausreichend genaue Ergebnisse.
. v = v1 + v2 ist also nur eine Näherungsformel. Für
geringe Geschwindigkeiten (wie sie auf der Erde üblich sind)
liefert sie jedoch ausreichend genaue Ergebnisse.
![m' = m / Wurzel aus [ 1 - (v² / c²) ]](fm.gif) Die Massenzunahme mit der Geschwindigkeit: Ein
Objekt mit der Masse m im Stillstand wird immer schwerer, je
schneller es sich relativ zu einem anderem Objekt bewegt. Die
Massenzunahme kann jedoch nur vom Beobachter ermittelt werden,
die Messung der eigenen Masse würde keine Veränderung ergeben!
Die Massenzunahme mit der Geschwindigkeit: Ein
Objekt mit der Masse m im Stillstand wird immer schwerer, je
schneller es sich relativ zu einem anderem Objekt bewegt. Die
Massenzunahme kann jedoch nur vom Beobachter ermittelt werden,
die Messung der eigenen Masse würde keine Veränderung ergeben!
Die Gleichwertigkeit von Masse und Energie: Die Energie, die in
einem Objekt steckt, hängt von seiner Masse ab. Wir wissen, daß
die Masse mit der Geschwindigkeit zunimmt. Folglich muß auch
die Energie zunehmen, weil zwei verschieden schwere Objekt bei
gleicher Geschwindigkeit auch eine verschieden hohe Energie
besitzen (potentielle oder kinetische Energie).
E = m *
c^2
Diese Formel besagt, wieviel Energie man maximal von
einer Masse erhält, wenn man die gesamte Masse in Energie
umwandeln würde. Würde dies gelingen, könnte man wenigen Tonnen
Masse die ganze Erde jahrelang mit Energie versorgen! Die
Atombombe ist ein trauriger Beweis dafür.
Unsere üblichen Energieerzeugungsformen geschehen durch chemische Prozesse, bei der nicht etwa die Masse in Energie umgewandelt wird, sondern nur eine Veränderung molekularen Struktur unter Abgabe von Energie erreicht wird (z. B. Verbrennung). Die Umwandlung von Masse in Energie geschieht jedoch durch sog. nukleare Prozesse.
Aus dieser Formel kann man auch schließen, daß Objekt mit irgendeiner Masse nicht einmal GENAU die Lichtgeschwindigkeit erreichen können, weil ihre Masse dann unendlich groß sein würde. Folglich müßte man für diese Beschleunigung auch unendlich viel Energie zuführen, also alle Energie des Universums plus noch mehr Energie!
Die spezielle Relativitätstheorie gilt nur bei Beschleunigung gleich null. Also konstanter Geschwindigkeit. Wir haben bereits festgestellt, das man nicht feststellen kann ob man sich mit konstanter Geschwindigkeit bewegt, ohne auf andere Punkte Bezug zu nehmen. Also ist Bewegung relativ und kann nicht absolut Bestimmt werden.
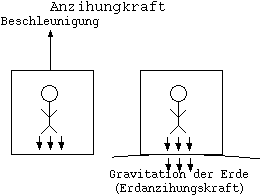 Wie sieht die aus, wenn ein man sich in einem geschlossenem Raum
befindet, welcher beschleunigt wird? Kann man feststellen, ob
dieser Raum beschleunigt wird? NEIN! Es ist nicht möglich
zwischen einer Beschleunigung und einer Gravitation
(Anziehungskraft z.B. auf der Erde) zu unterscheiden. Man könnte
nicht feststellen, ob sich der Raum auf der Erde steht oder sich
beschleunigend von dieser entfernt.
Wie sieht die aus, wenn ein man sich in einem geschlossenem Raum
befindet, welcher beschleunigt wird? Kann man feststellen, ob
dieser Raum beschleunigt wird? NEIN! Es ist nicht möglich
zwischen einer Beschleunigung und einer Gravitation
(Anziehungskraft z.B. auf der Erde) zu unterscheiden. Man könnte
nicht feststellen, ob sich der Raum auf der Erde steht oder sich
beschleunigend von dieser entfernt.
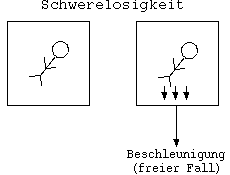 Das gegenteilige Experiment unterstützt diese Theorie: Man kann
nicht unterscheiden, ob sich der Raum in der Schwerelosigkeit
befindet oder auf einen Planeten fällt. Beide male verspürt man
in diesem Raum keine Gravitation. Ist ein Objekt im freiem Fall,
so herrscht auf diesem keine Gravitation, da alle Objekte in
diesem gleichermaßen angezogen werden.
Das gegenteilige Experiment unterstützt diese Theorie: Man kann
nicht unterscheiden, ob sich der Raum in der Schwerelosigkeit
befindet oder auf einen Planeten fällt. Beide male verspürt man
in diesem Raum keine Gravitation. Ist ein Objekt im freiem Fall,
so herrscht auf diesem keine Gravitation, da alle Objekte in
diesem gleichermaßen angezogen werden.
Das hier vorgestelle Prinzip ist bekannt unter dem Äquivalenzprinzip: Die Auswirkungen der Gravitation und einer Beschleunigungsbewegung sind gleichwertig und können nicht voneinander unterschieden werden.
Lichtstrahlen werden von Massen angezogen und ihre Laufbahn
dadurch gekrümmt!
Dies wurde mit einer Beobachtung eines verfrühten Sternaufgangs
bei einer Sonnenfinsternis bestätigt.
Interessant ist die Überlegung, wie groß und schwer ein Stern
sein müßte, um alle Lichtstrahlen in seiner Umgebung zu
verschlucken (schwarze Löcher!).
Die Berechnung der Lichtablenkung durch Massen erfolgt ebenfalls
durch die obige Formel der Massenanziehung. Voraussetzung ist,
daß Licht-Photonen ein Gewicht haben, solange sie in Bewegung
sind. Dies ist der Fall. Würden die Licht-Photonen jedoch
stillstehen, hätten sie keine Masse mehr (Restmasse 0, siehe
Formel der spezielle Relativitätstheorie!).
Gravitationsmassen verlangsamen den Zeitablauf. Je mehr Masse,
um so langsamer vergeht die Zeit!
Die Zeitverlangsamung wurde wie bei der speziellen
Relativitätstheorie mit der verlangsamten Vibration von Atomen
und der dadurch folgenden Rotverschiebung des Lichtes
nachgewiesen.
Bis zu seinem Tod im Jahre 1955 war Einstein dann mit der
Entwicklung der einheitlichen FT beschäftigt. Er hat diese
Theorie jedoch nie vollenden können.
Hierzu einige kurze Überlegungen (Auszug):
Massenanziehung: F = G * (m1 * m2) / d²
Anziehung zweier ungleicher Ladungen: (Coulomb-Gesetz)
F = C * (q1 * q2) / d²
Anziehung zweier ungleicher Magnetpole:
F = K * (M1 * M2) / d²
Diese drei Formeln drücken in mathematisch gleicher Weise drei
vollkommen unabhängige physikalische Phänomene.
Lediglich bei der Massenanziehung ist bisher keine Abstoßung
bekannt!!! (Antischwerkraft!?).
Historisch wurden diese Formeln vollkommen unabhängig
voneinander durch empirische Befunde entwickelt. Die ähnliche
Form der Formeln läßt jedoch den Schluß zu, daß alle drei
Phänomene einer gleichen natürlichen Gesetzmäßigkeit zugrunde
liegen. Die drei Formeln sind folglich nur Teilzweige einer
allgemeineren und grundlegenderen Naturgesetzlichen Formel.
Diese grundlegende Formel zu finden ist ein Teilbereich der
einheitlichen FT.
Der zweite Zweck ist jedoch weitaus größer als der erste. Es
ist der Versuch, ALLE PHYSIKALISCHEN PHÄNOMENE aus einigen
wenigen EINFACHEN UND GRUNDLEGENDEN PRINZIPIEN der Natur
abzuleiten.
|
Pages by Andreas Hofmeier |
 |
 Impressum/Note Datenschutzerklärung Impressum/Note Datenschutzerklärung |
|---|
|
http[s]://www.abmh.de/einstein/relativ/index.html |
|---|
 |
(c) Andreas B. M. Hofmeier This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 Germany License |