Pages by Andreas Hofmeier
 An-H
 eMail Impressum/Note Datenschutzerklärung
http[s]://www.abmh.de/fhs/GEL-L/Z72/Z72.HTML/index.html
Like to be free? ... then: Fight for Freedom

PDF Version LaTeX SRC

GEL Laborbericht
Versuch: Reihenschwingkreis

Andreas Hofmeier - Axel Schmidt

Zusammenfassung:

.



















Die Schaltung vierhielt sich bis auf kleinere Bauteil- und Messtoleranzen wie berechnet. Ziemlich genau bei der errechneten Resonanzfrequenz ( $ f_0 = 503Hz$) erhielten wir in beiden Messungen ein Maximum der Ausgangsspannung ($ U_{R_a}$). Daraus folgt, dass die Eigenschaft der Resonanzfrequenz nahezu ausschließlich von $ L$ und $ C$ bestimmt wird. Im Resonanzfall heben sich die Blindanteile des Kondensators und der Spule auf, der Scheinwiderstand ist am kleinsten. Bei $ R_a = 100\Omega$ erhielten wir eine erheblich größere maximale Ausgangspannung verglichen mit der Messung $ R_a = 400\Omega$. Bei $ R_a = 100\Omega$ ist allerdings die Bandbreite ($ \Delta f$) erheblich kleiner und $ f_c$ und $ f_L$ liegen näher zusamen, woraus folgt, dass die Güte größer/besser ist. Die Güte steigt mit kleinerwerdendem $ R_a$. Dies ist durch das Verhältnis von pendelnden Blindleistungen zwischen Spule und Kondensator zur Wirkleistung in $ R_{Cu} + R$ zu begründen.


Inhalt

Fragen

Warum ist es zweckmäßig die Eingangsspannung konstant zu halten?

Die Ausgangsspannung ist abhängig von der Frequenz, Eingangsspannung, Bauteileigenschaften (u.a. $ R$, $ C$, $ L$) und Umweltbedingungen (Temperatur, etc). Um vergleichbare Ergebnisse zu erhalten, muss alles konstant gehalten werden, bis auf die Eingangsgröße, von welcher abhängig man die Ausgangsspannung messen möchte.

Was versteht man unter den Begriffen Resonanzfrequenz, Bandbreite und Güte?

Bei der Resonanzfrequenz heben sich die Blindanteile der Spule und des Kondensators auf, so dass nur noch der Widerstand ($ R$ und $ R_{Cu}$) mit seinem realen Anteil übrig ist, also der imaginäre Anteil des Schwingkreises verschwindet. Im Resonanzfall ist der Scheinwiderstand am kleinsten.

Die Bandbreite ($ b_w$) ist definiert als Frequenzbereich, in dem die Schwingungsgröße größer oder gleich dem $ \frac{1}{\sqrt{2}}$'tel des Maximums dieser Größe ($ S_\varrho$) ist. In diesem Bereich liegt die Phasenverschiebung ($ \varphi$) zwischen der Schwingungsgröße und der Eingangsgröße betragsmäßig unter 45°.

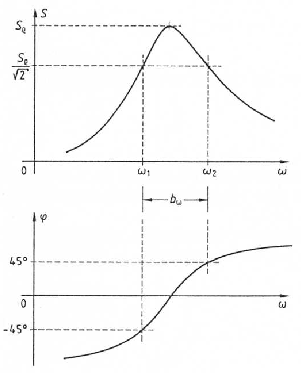
\begin{figure}\centerline{\epsffile{Z72.Guete.eps}}\end{figure}



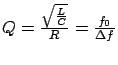
Die Güte, welche das Verhältnis von pendelnden Blindleistungen zwischen Spule und Kondensator zur Wirkleistung darstellt, kann durch das Verhältnis von Kennleitwert zu Wirkleitwert errechnet werden. Der Kennleitwert ist $ \sqrt{L/C}$. Der Wirkleitwert ist der Kehrwert des bei der gefragten Frequenz gemessenen Widerstandes. Also $ Q = \frac{\sqrt{\frac{L}{C}}}{R} = \frac{f_0}{\Delta f}$

Berechnung mit den gegebenen Werten

Gegebenen Werte: $ U_E = 1V$, $ L = 200mH$, $ C = 500nF$, $ R_a = 100\Omega$, $ R_a' = 400\Omega$

berechnete Frequenzen


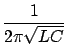$\displaystyle f_0$ $\displaystyle =$ $\displaystyle \frac{1}{2 \pi \sqrt{L C}}$  
       
$\displaystyle f_0$ $\displaystyle =$ $\displaystyle 503.29 \:Hz$  


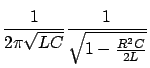$\displaystyle f_{0L}$ $\displaystyle =$ $\displaystyle \frac{1}{2 \pi \sqrt{L C}} \frac{1}{\sqrt{1-\frac{R^2 C}{2L}}}$  
       
$\displaystyle f_{0L_{100\Omega}}$ $\displaystyle =$ $\displaystyle 506,46 \:Hz$  
$\displaystyle f_{0L_{400\Omega}}$ $\displaystyle =$ $\displaystyle 562,69 \:Hz$  


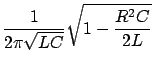$\displaystyle f_{0C}$ $\displaystyle =$ $\displaystyle \frac{1}{2 \pi \sqrt{L C}} \sqrt{1-\frac{R^2 C}{2L}}$  
       
$\displaystyle f_{0C_{100\Omega}}$ $\displaystyle =$ $\displaystyle 500,13 \:Hz$  
$\displaystyle f_{0C_{400\Omega}}$ $\displaystyle =$ $\displaystyle 450,15 \:Hz$  

Versuchsdurchführung

$ R_a = 100\Omega$ (mit Multimetern gemessen)

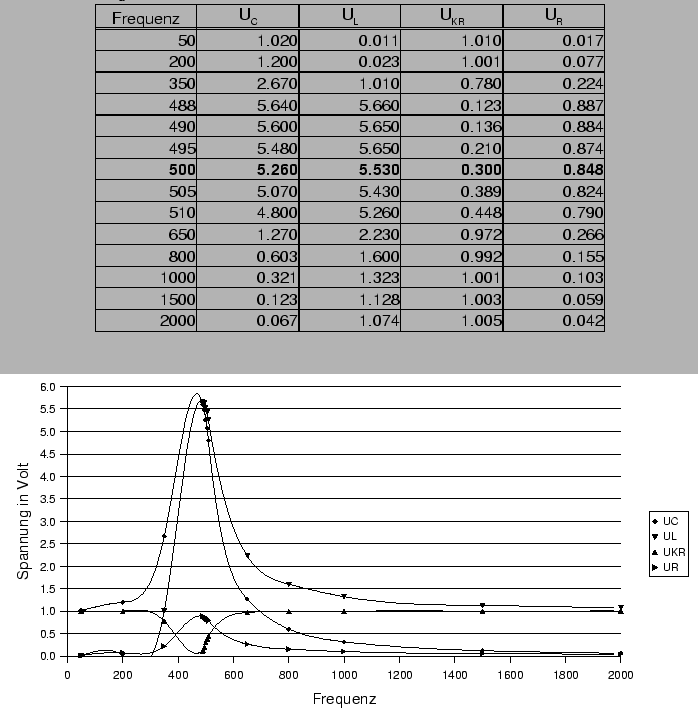
\begin{figure}\centerline{\epsffile{Z72.100.eps}}\end{figure}

Phasenverschiebung und Zeigerdiagramme

Ablesen der Werte aus den gemessenen Werten erfolgte über lineare Interpolation.

$ U_A = U_R \thickapprox \frac{1}{\sqrt{2}} 0,874V \thickapprox 0.618V$
$ f_1 \thickapprox \frac{(488-350)Hz}{(0.887-0.224)V}*(0.618-0.244)V + 350Hz \thickapprox 428Hz$
$ U_{f1_C} \thickapprox 4,35V$
$ U_{f1_L} \thickapprox 3,64V$
$ \alpha_1 \thickapprox ArcCos\frac{U_a}{U_0} = ArcCos\frac{0,874V}{1V} = -39°$
$ \alpha_1' \thickapprox \alpha_1 \thickapprox ArcTan\frac{U_{f1_L} - U_{f1_C}}{U_A} = ArcTan\frac{-0.89V}{0.874V} = -46°$

$ f_2 \thickapprox \frac{(510-650)Hz}{(0.790-0.266)V}*(0.618-0.266)V + 650Hz \thickapprox 556Hz$
$ U_{f2_C} \thickapprox 3,64V$
$ U_{f2_L} \thickapprox 4,26V$
$ \alpha_2' \thickapprox -\alpha_1 \thickapprox ArcTan\frac{U_{f1_L} - U_{f1_C}}{U_A} = ArcTan\frac{0.62V}{0.874V} = 35°$
$ f_B = \Delta f \thickapprox f_2 - f_1 = 556Hz - 428Hz = 128Hz$

Die relativ große Abweichung der Winkel voneinander ist durch Meßungenauigkeiten und Approximation der Werte auf Basis der Meßwerte zu erklären.

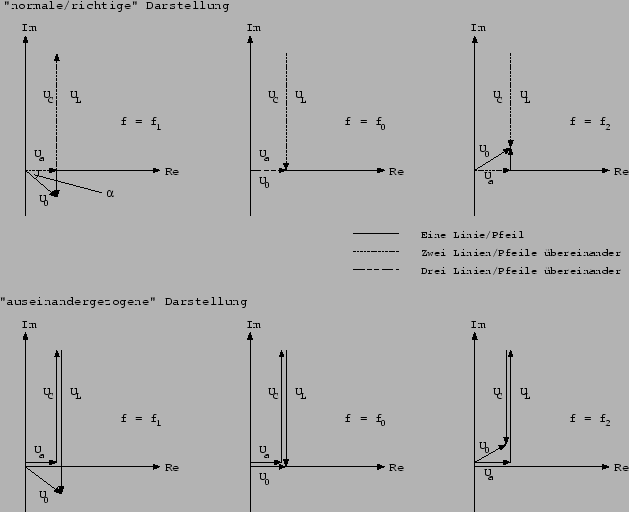
\begin{figure}\centerline{\epsffile{Z72.ZGD.eps}}\end{figure}

$ R_a = 400\Omega$ (mit PC gemessen)

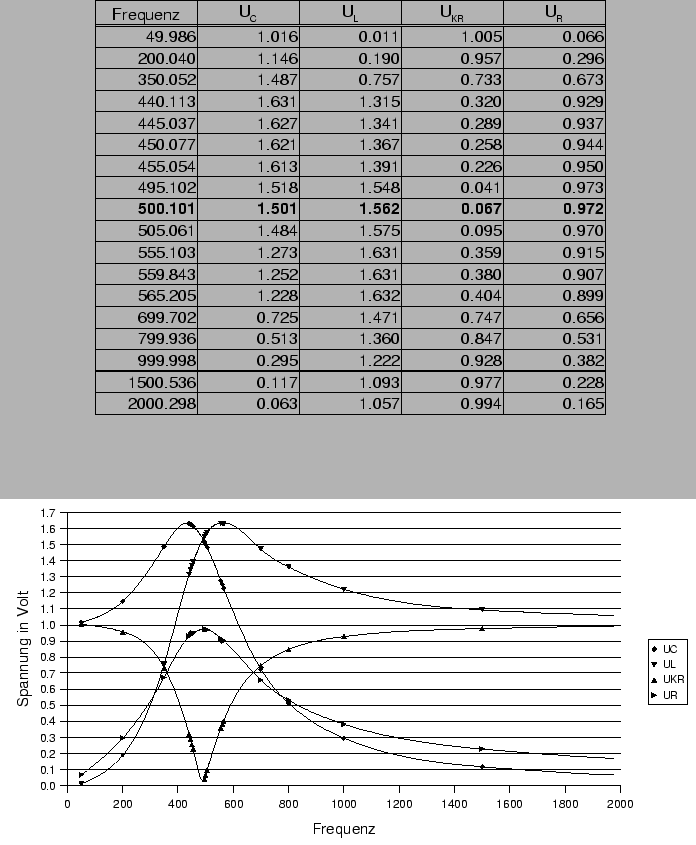
\begin{figure}\centerline{\epsffile{Z72.400.eps}}\end{figure}

Güte

$ \frac{1}{\sqrt{2}} 0,973V = 0.688V$
$ f_1 \thickapprox \frac{(440-350) Hz}{(0.929-0.673) V}*(0.688-0.673) V + 350Hz \thickapprox 355Hz$
$ f_2 \thickapprox \frac{(565-699) Hz}{(0.899-0.656) V}*(0.688-0.656) V + 699Hz \thickapprox 681Hz$
$ f_B = \Delta f \thickapprox f_2 - f_1 = 681Hz - 355Hz = 326Hz$

$ Q_{L_{100}} = \frac{f_0}{\Delta f} = \frac{f_0}{f_2 - f_1} \thickapprox \frac{503Hz}{556Hz - 428Hz} \thickapprox 3.93$
$ Q_{L_{400}} = \frac{f_0}{\Delta f} = \frac{f_0}{f_2 - f_1} \thickapprox \frac{503Hz}{681Hz - 355Hz} \thickapprox 1.54$

Errechnete Güte aus gegebenen Bauteilwerten
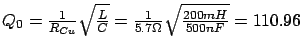
$ Q_0 = \frac{1}{R_{Cu}}\sqrt{\frac{L}{C}} = \frac{1}{5.7\Omega}\sqrt{\frac{200mH}{500nF}} = 110.96$
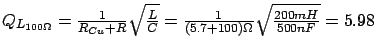
$ Q_{L_{100\Omega}} = \frac{1}{R_{Cu} + R}\sqrt{\frac{L}{C}} = \frac{1}{(5.7 + 100)\Omega}\sqrt{\frac{200mH}{500nF}} = 5.98$

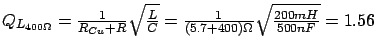
$ Q_{L_{400\Omega}} = \frac{1}{R_{Cu} + R}\sqrt{\frac{L}{C}} = \frac{1}{(5.7 + 400)\Omega}\sqrt{\frac{200mH}{500nF}} = 1.56$

Die gemessenen Werte der Lastgüte stimmen bei der PC-Messung sehr gut mit den berechneten Werten überein. Bei der Messung mit Hilfe der Multimeter ist eine erhebliche Abweichung erkennbar. Daraus ist zu folgern, das die Messung mit Hilfe des PCs genauer ist, vorallem da die Frequenz ebenfalls gemessen wurde. Die Güte steigt mit sinkendem $ R_a$ und erreicht ihr Maximum bei $ R_a = 0\Omega$, welches praktisch nicht erreicht werden kann. Dieses Verhalten ist durch die Definition der Güte zu erklären: Je kleiner $ R_a$ ist, umso kleiner die Wirkleistung. Güte = Verhältnis von pendelndender Blindleistung zu Wirkleistung.

Aus gemessenen Werten Abgelesene Frequenzen:
$ f_0 \thickapprox 500Hz$
$ f_C \thickapprox 440Hz$
$ f_L \thickapprox 565Hz$

PDF Version LaTeX SRC

Pages by Andreas Hofmeier
 An-H
 eMail Impressum/Note Datenschutzerklärung
http[s]://www.abmh.de/fhs/GEL-L/Z72/Z72.HTML/index.html
Creative Commons License
(c) Andreas B. M. Hofmeier
This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 Germany License