Pages by Andreas Hofmeier
 An-H
 eMail Impressum/Note Datenschutzerklärung
http[s]://www.abmh.de/fhs/EMT-L/FM_Hofmeier/FM.HTML/index.html
Like to be free? ... then: Fight for Freedom

PDF Version LaTeX SRC

EMT Laborbericht
Versuch: FM
Fernmessung

Andreas Hofmeier

Auftraggeber: Prof. Dr.-Ing. M. Mevenkamp,
  Fachhochschule Bremen
Durchführung seit: 01.07.2002
Ort der Durchführung: FH Bremen, Neustadtswall 30,
  Raum: E502
Ausgewertete Ergebnisse vom 01.07.2002 bis 30.06.2003
Abgabe am: 14.01.2004

Team B4

Andreas Hofmeier     ___________________
       
Axel Schmidt     ___________________
       
Y.Fabrice Fodouop     ___________________

Zusammenfassung:

.
In diesem Versuch wurden mit Hilfe eines Fernmesssystems Umweltgrößen (Temperatur und Lichteinstrahlung) über das Internet erfasst und ausgewertet. Dazu war es nötig sich mit Signalaufbereitung mit Hilfe von Operationsverstärkern, elektrischer Meßtechnik, analog nach digital Umsetzern und einigen GNU UNIX/Linux Texttools auseinanderzusetzen.

Es hat sich herausgestellt, dass ein LDR im Vergleich zu einer Solarzelle zur Messung der Lichteinstrahlung ungeeignet ist. Er unterscheidet lediglich zwischen hell und dunkel und ist erheblich träger als die Solarzelle. Die untersuchten Tageslängen stimmten erstaunlich genau mit einer Kosinusfunktion überein.

Die thermisch Zeitkonstante des Raumes E502 wurde auf ca. 9h festgelegt.


Inhalt

Versuchsziele

In diesem Versuch, bei welchem Umweltgrößen (Temperatur und Lichteinstrahlung) mittels eines Fernmesssystems über das Internet gemessen wurden, standen folgende Punkte auf dem Plan:

-
Messen von Umweltgrößen mittels der elektrischen Meßtechnik
-
Signalaufbereitung mit Hilfe von Operationsverstärkern
-
Digitalisierung der Meßwerte für den Computer
-
Technologien des Fernmessens
-
Verarbeitung großer Mengen an Meßdaten mit UNIX/GNU Linux-Standard-Text-Tools

Grundlegender Versuchsaufbau - Übersicht

Im fünften Stock des E-Traktes der Hochschule Bremen am Standort Neustadtswall (53,04° nördl. Breite, 8,49° östl. Länge) wurde im Raum 502 ein automatisches Meßerfassungssytem installiert. Dieses System erfasst alle zwei Minuten die Lichteinstrahlung, die Innen- und Außentemperatur.

Temperaturmessung

Versuchsaufbau

Zwecks Temperaturmessung wurden zwei PTCs ( - Widerstände, welche mit steigender Temperatur steigende Werte aufweisen; Modell: KTY 10-6) angebracht. Die Außentemperatur wird einige Zentimeter vor dem Fenster gemessen. Die Innentemperatur wird in einer Höhe von einem Meter (ab Fußboden 5. Stock) und einem Meter vom Fenster entfernt aufgenommen.

Störgrößen

Die Außentemperaturmessung wird durch Sonneneinstrahlung und Witterung beeinträchtigt. Durch Sonneneinstrahlung wird der Sensor erwärmt und misst daher eine zu hohe Temperatur. Durch Regen und Wind findet eine Abkühlung statt, was dazu führt, dass der Sensor einen zu niedrigen Wert meldet. Zusätzlich wird der Außensensor ab ca. 08:30 von der Sonne beschienen. Dieser Zeitpunkt verschiebt sich allerdings mit der Jahreszeit.

Die Innentemperaturmessung wird nur durch Sonneneinstrahlung und das Aufdrehen der Heizung gestört. Der Innensensor wird in einem Zeitraum von ca. 11 bis 12 Uhr von der Sonne beschienen. Diese Zeitspanne verschiebt sich allerdings mit der Jahreszeit.

Ein weiterer unbekannter systematischer Fehler liegt in der Toleranz der verwendeten Widerstände. Der durch die Abtastrate verursachte Fehler kann auf Grund der Trägheit der Temperaturmessung vernachlässigt werden. Zusätzlich treten hier zufällige Fehler in Form von elektrischen Störeinstrahlungen und Meßunsicherheit auf.

Brückenschaltung zur Bestimmung der Werte der temperaturabhängigen Widerstände

Der Widerstand $ R_\vartheta$ (bzw. die Temperatur) wird über eine Brückenschaltung gemessen. Eine Brückenschaltung besteht aus zwei voneinander unabhängigen Spannungsteilern, wobei einer der vier Widerständen in der Brücke der zu messende ist. Ist die Brücke abgeglichen, sind die Widerstandsverhältnisse $ \frac{R_1}{R_\vartheta}$ und $ \frac{R_3}{R_4}$ gleich. Die Ausgangsspannung, die Spannungsdifferenz zwischen den Spannungsteilern (hier $ U_n - U_p$), beträgt 0V.

Verändert sich nun der zu messende Widerstand ( $ R_\vartheta$), ändert sich das Widerstandsverhältnis und somit verschiebt sich die Spannung ($ U_p$) am Spannungsteiler ($ R_1$ und $ R_\vartheta$). Da der andere Spannungsteiler stabil bleibt, ist die Ausgangsspannung nicht länger null.

Beim Aufbau wurden folgende Bauteilgrößen verwendet: $ R_v = 8.25k\Omega$,
$ R_r = 100k\Omega$, $ R_1 = 14.98k\Omega$, $ R_3 = 14.98k\Omega$, $ R_4 =1.44k\Omega$, $ U_{Stabil} = 5.10V$

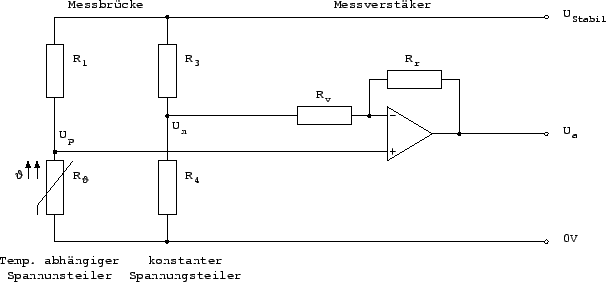
\begin{figure}\centerline{\epsffile{Temp.eps}}\end{figure}

Um den Meßfehler, der entsteht wenn der Temperaturabhängige Spannungsteiler ($ R_1$ und $ R_\vartheta$) belastet wird, so gering wie möglich zu halten, wird dieser Meßpunkt ($ U_p$) direkt in den $ +$ Eingang des OPs geführt - dieser hat theoretisch einen unendlich hohen Eingangswiderstand, er belastet also den Spannungsteiler nicht.

Die Verstärkung des OPs wird über $ R_v$ und $ R_r$ eingestellt. Dadurch wird der Innenwiderstand des gesamten $ -$ Einganges (also $ R_{-_{ges}} = R_v + R_{-} \parallel R_{r_{Schein}}$) erheblich reduziert, was dazu führt, dass sich die Spannung $ U_n$ am konstanten Spannungsteiler verschiebt.

Die Ausgangsspannung $ U_a$ wird in den AD-Umsetzer, also in den Computer geleitet.

Theoretische Berechnung

Der Ideale Operationsverstärker

Um den Verstärker, welcher mit Operationsverstärkern aufgebaut ist, errechnen zu können wurden folgende theoretischen Annahmen getroffen:

-
Die Eingangswiderstände des Operationsverstärkers sind unendlich groß, es fließt also kein Strom durch sie in den Operationsverstärker.

-
Der Operationsverstärker wird im analogen Bereich betrieben. Die Ausgangsspannung wird also nie in die Begrenzung getrieben: $ -U_s < U_a < U_s$

-
Die Verstärkung des Operationsverstärkers ist Unendlich groß: $ V = \infty$

-
Der Operationsverstärker ist ein Differenzverstärker. Er verstärkt also die Differenz der Eingangsspannungen: $ U_a = V(U_{e_+} - U_{e_-})$. Ist V aber unendlich, gibt es nur drei mögliche Ausgangsspannungen:

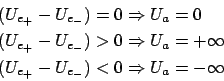\begin{displaymath}\begin{split}(U_{e_+} - U_{e_-}) = 0 & \Rightarrow U_a = 0 \\... ...(U_{e_+} - U_{e_-}) < 0 & \Rightarrow U_a = -\infty \end{split}\end{displaymath}    

Ein realer Operationsverstärker kann natürlich keine unendlich hohe Spannung rausgeben. Die Ausgangsspannung ist durch seine Betriebsspannung begrenzt. In diesem Fall wurde der Operationsverstärker ``in die Begrenzung gefahren'', also als Schalter (z.B. Schmitttrigger) verwendet.

Daraus folgt, dass wenn wir den Operationsverstärker als analogen Verstärker betreiben wollen, die Differenzspannung $ (U_{e_+} - U_{e_-})$ gleich null sein muss.

Vereinfachte OP-Verstärkerschaltung

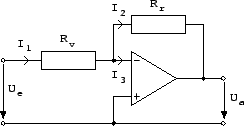
Zur einfachen Bestimmung der Verstärkung wurde hier angenommen, dass der $ +$ Eingang des OPs auf Masse (also 0V-Potential) liegt.

[1cm]

\begin{figure}\centerline{\epsffile{OPv.eps}}\end{figure}

$ I_1 = I_2 + I_3$
$ I_3 = 0 \Rightarrow I_1 = I_2$
$ U_{+-} = 0 \Rightarrow U_- = 0V$
$ I_1 = \frac{U_e - U_-}{R_v} = \frac{U_e}{R_v}$
$ U_a = - I_1 R_r = - \frac{R_r}{R_v}U_e$

$ V = \frac{U_a}{U_e} = \frac{R_r}{R_v} = 12 \frac{4}{33} \approx 12.12$

Die verwendete OP-Verstärkerschaltung

In diesem speziellen Fall verhält sich die Ausgangsspannung etwas anders als $ U_a = V U_e$, da der $ +$ Eingang nicht auf Masse liegt und so den $ -$ Eingang auf ein höheres Niveau zieht:

[1cm]

\begin{figure}\centerline{\epsffile{OPv2.eps}}\end{figure}

$ U_{+-} = 0 \Rightarrow I_1 = \frac{U_n - U_p}{R_v}$
$ U_{R_r} = - I_1 R_r = - \frac{R_r}{R_v}(U_n - U_p)$

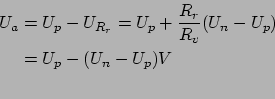\begin{displaymath}\begin{split}U_a &= U_p - U_{R_r} = U_p + \frac{R_r}{R_v}(U_n - U_p) \\ &= U_p - (U_n - U_p)V\\ \\ \end{split}\end{displaymath}    

Ersatzspannungsquelle für konstanten Spannungsteiler

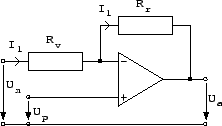
Um die Ausgangsspannung in Abhängigkeit von der Eingangsspannung ($ U_p$) errechnen zu können muss die Spannung am $ +$ Eingang bestimmt werden. Würde man ``einfach'' einen unbelasteten Spannungsteiler ($ R_3$, $ R_4$) annehmen, würde man wie bereits weiter oben abgehandelt einen Fehler machen.

Um diesen Fehler zu umgehen, rechnet man den Spannungsteiler in eine Ersatzspannungsquelle um:

[1cm]

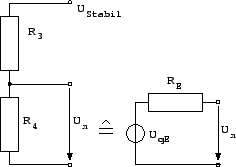
\begin{figure}\centerline{\epsffile{OPvErsSpQ.eps}}\end{figure}

$ U_{qE} = \frac{R_4}{R_3 + R_4} U_{Stabil} \approx 0.447V$

$ R_E = R_3 \parallel R_4 = \frac{R_3 R_4}{R_3 + R_4} \approx 1.31k\Omega$

Diese Ersatzspannungsquelle wird nun mit der Verstärkerschaltung verbunden:

[1cm]

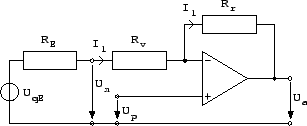
\begin{figure}\centerline{\epsffile{OPvErs.eps}}\end{figure}

$ I_1 = \frac{U_{qE} - U_p}{R_E + R_v} = \frac{U_p - U_a}{R_r}$

$ \small {U_{qE} R_r \underline{- U_p R_r} = \underline{U_p R_E + U_p R_v} - U_a R_E - U_a R_v}$

$ \small {(R_E + R_v + R_r) U_p = (R_E + R_v) U_a + R_r U_{qE}}$

$ U_p = \frac{R_E + R_v}{R_E + R_v + R_r} U_a + \frac{R_r}{R_E + R_v + R_r} U_{qE}$

Durch weiteres Umstellen und Einsetzen der bereits hergeleiteten Formeln können wir die noch unbekannten Zusammenhänge aufdecken:

-
Die Ausgangsspannung und die Brückenspannung (Spannungsdifferenz zwischen den beiden Spannungsteilern):

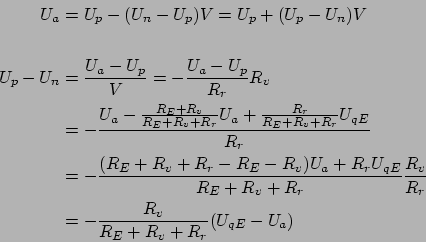\begin{displaymath}\begin{split}U_a &= U_p - (U_n - U_p) V = U_p + (U_p - U_n) V... ...\\ &= - \frac{R_v}{R_E + R_v + R_r} (U_{qE} - U_a) \end{split}\end{displaymath}    

Übertragungsverhalten Temperatur nach Spannung

-
Die Spannung am PTC in Abhängigkeit von der Ausgangsspannung der gesamten Stufe:

$ U_p(U_a) = \frac{R_E + R_v}{R_E + R_v + R_r} U_a + \frac{R_r}{R_E + R_v + R_r} \frac{R_4}{R_3 + R_4} U_{Stabil}$

-
Zusammenhang des Widerstandes des PTCs und der Spannung, welche an ihm abfällt:

$ U_p(R_\vartheta) = \frac{R_\vartheta}{R_1 + R_\vartheta} \Rightarrow R_\varthe... ...) = \frac{U_p}{U_{Stabil} - U_p} R_1 = \frac{1}{\frac{U_{Stabil}}{U_p} - 1} R_1$

Setzt man diese beiden Formeln in einander ein, so erhält man eine Übertragungsfunktion von Temperatur zu Spannung ($ U_a$):

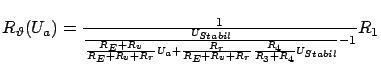
$ R_\vartheta(U_a) = \frac{1}{\frac{U_{Stabil}}{\frac{R_E + R_v}{R_E + R_v + R_r} U_a + \frac{R_r}{R_E + R_v + R_r} \frac{R_4}{R_3 + R_4} U_{Stabil}} - 1} R_1$

Aus dem Datenblatt für den Temperatursensor (PTC) Modell KTY-6:

$ R_{25} = [1980 ... 2020] \approx 2000$

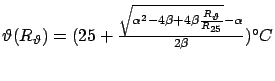
[1cm] $ \vartheta(R_\vartheta) = (25 + \frac{\sqrt{\alpha^2 - 4 \beta + 4 \beta \frac{R_\vartheta}{R_{25}}} - \alpha}{2 \beta}) °C$

$ \alpha = 7.88 10^{-3} K^{-1}$
$ \beta = 1.937 10^{-5} K^{-2}$

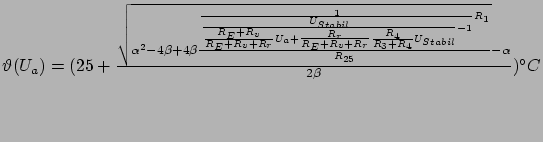
$ \vartheta(U_a) = (25 + \frac{\sqrt{\alpha^2 - 4 \beta + 4 \beta \frac{\frac{1}... ..._r} \frac{R_4}{R_3 + R_4} U_{Stabil}} - 1} R_1}{R_{25}}} - \alpha}{2 \beta}) °C$

Lineare Näherung des Übertragungsverhaltens von Temperatur nach Spannung

Um eine lineare Näherungsformel zu bestimmen braucht man zwei Punkte:

-
$ U_a = 0V \Rightarrow U_p \approx 0.408V \Rightarrow R_\vartheta \approx 1.30k\Omega \Rightarrow \vartheta \approx -25.5 °C$

Maximaler Strom durch PTC: $ I_{max} = \frac{U_{Stabil}}{R_1 + R_{\vartheta_{min}}} = 0.313mA$.

-
$ U_a = 5V \Rightarrow U_p \approx 0.845V \Rightarrow R_\vartheta \approx 2.97k\Omega \Rightarrow \vartheta \approx 79.5 °C$

Minimaler Strom durch PTC: $ I_{min} = \frac{U_{Stabil}}{R_1 + R_{\vartheta_{max}}} = 0.284mA$ Eine Korrektur des durch den vom Strom verursachten Fehlers kann hier wegfallen. Die aus der Kennlinie (aus PTC-Datenblatt: $ \frac{\Delta R}{\Delta I}$) abgelesene Toleranz von ca. $ -0.6\%$ für den um ca. $ 0.7mA$ zu kleinen Strom (AP: $ 1mA$) ist vernachlässigbar gering.

Womit man jetzt die lineare Näherungsfunktion (Gerade) bestimmen kann:

[1cm] Temperatur $ \rightarrow$ Ausgangsspannung

$ U_a(\vartheta) = m_1 \vartheta + b_1$

$ m_1 = \frac{\Delta U_a}{\Delta \vartheta} = \frac{U_{a_{max}} - U_{a_{min}}}{\vartheta_{max} - \vartheta_{min}} \approx 0.0476 \frac{V}{°C}$

$ b_1 = -\vartheta_{min} m_1 + U_{a_{min}} \approx 1.21V$

$ U_a(\vartheta) = 0.0476 \frac{V}{°C} \vartheta + 1.21V$

Ausgangsspannung $ \rightarrow$ Temperatur

$ \vartheta(U_a) = m_2 U_a + b_2$

$ m_2 = \frac{\Delta \vartheta}{\Delta U_a} = \frac{\vartheta_{max} - \vartheta_{min}}{U_{a_{max}} - U_{a_{min}}} \approx 20.99 \frac{°C}{V}$

$ b_2 = -\vartheta_{min} m_2 + U_{a_{min}} \approx -25.46V$

$ \vartheta(U_a) = 20.99 \frac{°C}{V} U_a - 25.46 °C$

Die Steigung der Funktionen ist gleichzeitig die Empfindlichkeit der Messung. Da die Übertragung in beide Richtungen funktionieren muss, sind die Funktionen invers zueinander. Es gilt $ x = U_a(\vartheta(x))$ Da es sich um Geraden handelt, gilt: $ m_1 m_2 = 1$

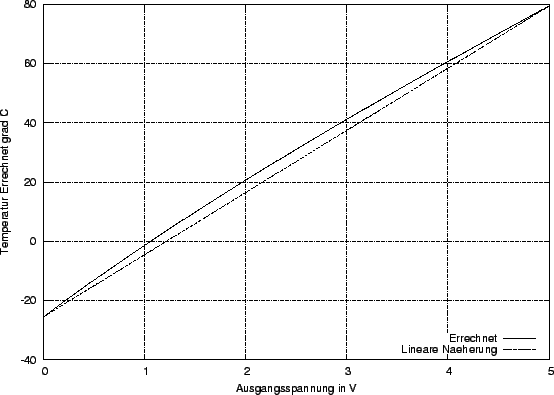
Links: Der Ausgangsspannungs-Temperatur-Zusammenhang. Zum Vergleich die lineare Näherung und die errechnete Übertragung.

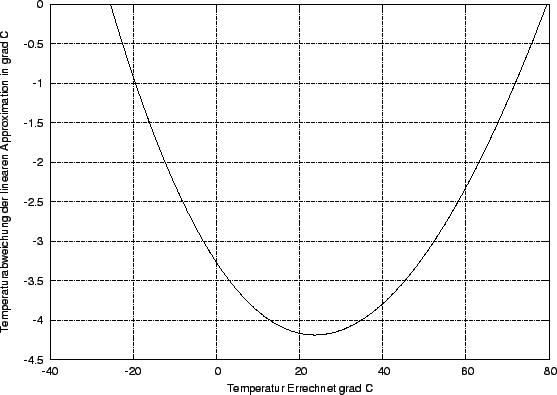
Da die Übertragungsfunktion eben nicht ganz linear ist (etwas nach oben ``Ausgebeult'') liefert die lineare Näherung zu geringe Werte. Die Abhängigkeit des Fehlers von der errechneten Temperatur wird rechts dargestellt. Er erreicht sein Maximum von $ -4.18°C$ bei $ 24°C$.

\begin{figure}\centerline{\epsffile{Ua2T.Werte.eps} }\end{figure}

\begin{figure}\centerline{\epsffile{Ua2T.Diff.eps} }\end{figure}














Der Analog-Digital-Umsetzer

Der AD-Wandler (Atmel 89C2051) hat eine Auflösung von 10 Bit über eine Spannung von 5V. Die Amplitudenauflösung beträgt daher:

$ U_{step} = \frac{U_{ref}}{2^n - 1} = \frac{5}{1023} \approx 4.8mV$

Umrechnung der Meßwerte

Die Meßwerte werden in Form von Hexadezimalzahlen gespeichert und müssen zur weiteren Verarbeitung in das Dezimalsystem umgewandelt werden. Der Zahlenbereich geht von 0 bis $ 2^{10} - 1 = 1023$, was einer Spannung von $ 0V$ bis $ 5V$ entspricht. Die Dezimalwerte können folgendermaßen in die Spannung umgerechnet werden, wobei in unserem Fall $ m$ der Dezimalwert und $ U_{ref} = 5V$ sind:

$ U_a(m) = \frac{m}{2^{10} - 1} U_{ref}$

Verwendet man die lineare Näherung, wird der Dezimalwert mit dieser Formel in die Temperatur umgewandelt:

$ \vartheta(U_a(m)) = 20.99 \frac{°C}{V} \frac{U_{ref}}{2^{10} - 1} m - 25.46 °C = 0.1026 m °C - 25.46 °C$

Die Auflösung beträgt also $ 0.1026 \frac{°C}{Schritt}$. Sie kann auch direkt bestimmt werden: $ \frac{\vartheta_{max}-\vartheta_{min}}{2^n - 1} \approx \frac{105°C}{1023} \approx 0.1026\frac{°C}{Schritt} = 0.1026\frac{K}{Schritt}$ Da es sich hier um Temperaturdifferenzen (Bereiche) handelt, können diese sowohl in $ °C$ als auch in $ K$ angegeben werden.

Diese Angaben gelten nur für die lineare Näherung. Bei der tatsächlichen Übertragung ist die Schrittweite nicht konstant, da die Übertragung der Temperatur zur Ausgangsspannung nicht linear ist.

In unserem Fall wird ein Bereich von $ -25.5°C$ bis $ 79.5°C$ auf 0 bis $ 5V$ abgebildet. Wenn man von einem tatsächlichem Temperaturbereich von $ -20°C$ bis $ 50°C$ ausgeht, bleiben die Bereiche $ -25.5°C$ bis $ -20°C$ und von $ 50°C$ bis $ 79.5°C$ ungenutzt. Geht man von der linearen Übertragung aus, so werden ``nur'' $ \frac{2}{3}$ also ca. $ 66.6\%$ des Wertebereiches ausgenutzt. Das restliche drittel bleibt ungenutzt.

Auswertung

Monatsübersicht April

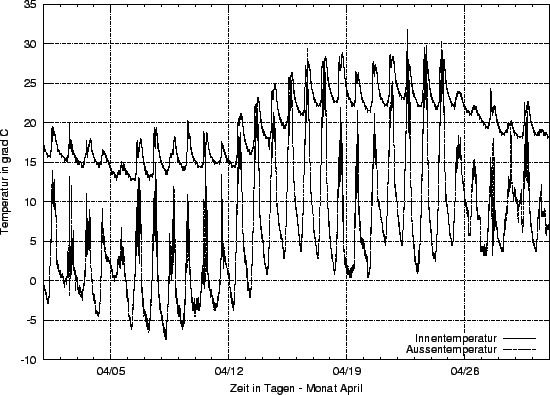
Im folgendem Diagramm wurde der Temperaturverlauf im Monat April 2003 dargestellt. Die Extremwerte der Innen- und Außentemperatur liegen zeitlich gesehen übereinander. Es ist deutlich zu sehen, dass sich die Innentemperatur wie die Außentemperatur verhielt. Daraus kann gefolgert werden, dass beide Temperaturen von der selben Ursache (der Sonneneinstrahlung) beeinflusst wurden. Die Tageshöchstwerte wurden um ca. 13:30 erreicht und die Tagesminimalwerte um etwa 6:00. Die Innentemperatur bewegte sich in einem Bereich zwischen 13°C und 29°C. Während sich die Außentemperatur zwischen -7°C und 32°C bewegte.

\begin{figure}\centerline{\epsffile{APRIL.temp.11.eps} }\end{figure}

Thermische Zeitkonstante 11./12. April

Um die thermische Zeitkonstante des Raumes E502 zu bestimmen, wurde ein Abkühlungsvorgang aus der Temperaturkennlinie herausgegriffen: Von Freitag den 11. April 14:15 bis Samstag den 12. April 9:00. Es fand sich leider kein Abschnit, der zur Bestimmung über drei Tage geeignet gewesen wäre.

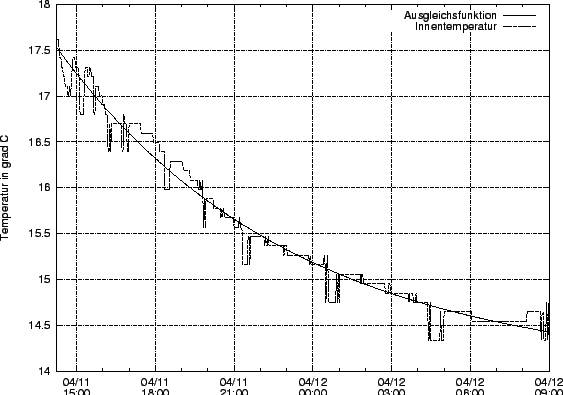
\begin{figure}\centerline{\epsffile{APRIL.temp.11b.eps} }\end{figure}

Mit Hilfe der FIT-Funktion von Gnuplot wurde eine Ausgleichs-E-Funktion hinein gelegt:

$ \vartheta(t) = 3.55°C * e^{-\frac{t}{\tau}} + 14°C$ mit $ \boxed{\tau = 8.99h}$

Messung der Lichteinstrahlung

Mit Hilfe der Solarzelle

Versuchsaufbau

Die polykristalline (= bestehend aus mehreren Kristallen) Solarzelle mit einer Fläche von $ 80 * 50 mm^2$ wurde von innen an der wärmedämmenden Fensterscheibe befestigt. Ihre Ausgangsspannung wird direkt in den ADU, also in den Computer geleitet.

Die Solarzelle wird ab ca. 9:00 von der Sonne beschienen. Sie hat eine maximale Leerlaufspannung von $ U_{0C} = 0.6V$.

Die Abtastrate von ``nur'' aller zwei Minuten stellt hier eine mögliche Fehlerquelle dar, da die Solarzelle sehr schnell auf die Änderung der Lichteinstrahlung reagiert. Aus diesem Grund werden Extremwerte möglicherweise abgeschnitten und der Verlauf der Itensität der Lichteinstrahlung nicht naturgetreu dargestellt.

Betrachtung der Meßergebnisse

[1cm]

\begin{figure}\centerline{\epsffile{Solarverteilung.eps} }\end{figure}



Dieses Histogramm enthält alle Meßwerte welche in dem von mir bearbeiteten Zeitabschnitt gemessen wurden. Die Anzahl der 0-Werte wurde abgeschnitten um die restliche Verteilung besser darstellen zu können. Sie ist bei etwas über 100000 anzusiedeln.

An der Solarzelle wurde eine maximale Spannung von $ U_{max} = 0.26V$ und eine minimale Spannung von $ U_{min} = 0V$ gemessen. Somit wurden etwa $ 5\%$ des Wertevorrates des ADUs genutzt.

Mit den Annahmen, dass die Sonneneinstrahlung zwischen 0 und $ 1000\frac{W}{m^2}$ schwankt und sich die Übertragung linear verhält (der nicht senkrechte Einstrahlungswinkel die Linearität nicht sonderlich beeinflusst) kann die Sonneneinstrahlung linear approximiert werden. Wobei $ U$ die gemessene Spannung und $ P$ die daraus resultierende Sonneneinstrahlungsleistung darstellt:

$ P(U) = \frac{U}{U_{max}} P_{max} = 3846 \frac{W}{V} U$

Mit Hilfe des LDRs

Versuchsaufbau

Die Lichteinstrahlung wird zusätzlich mit einem LDR (Light Dependent Resistor) gemessen, welcher neben der Solarzelle angebracht ist. Der durch die Abtastrate hervorgerufene Fehler kann auf Grund der Trägheit des LDRs vernachlässigt werden.

[1cm]

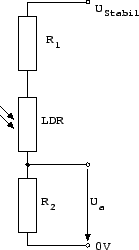
\begin{figure}\centerline{\epsffile{LDR.eps}}\end{figure}

Mit Hilfe dieses Spannungsteilers wird der Widerstandswert des LDRs gemessen.

Beim Aufbau wurden diese Bauteile verwendet: $ R_1 = 430\Omega$, $ R_2 = 1k\Omega$,

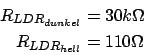\begin{displaymath}\begin{split}R_{LDR_{dunkel}} &= 30k\Omega\\ R_{LDR_{hell}} &= 110\Omega \end{split}\end{displaymath}    

Die Ausgangsspannung ($ U_a$) wurde direkt auf den Eingang des ADUs gegeben. $ U_{Stabil} = 5.1V$

Zusammenhang zwischen dem Widerstand des LDRs und der Ausgangsspannung:

$ U_a(R_{LDR}) = \frac{R_2}{R_1 + R_{LDR} + R_2} U_{Stabil}$

Der Spannungsbereich, auf den die Sonneneinstrahlung abgebildet wird kann durch Einsetzen der beiden Randwerte des LDRs ermittelt werden:

$ U_{a_{min}} = \frac{R_2}{R_1 + R_{LDR_{dunkel}} + R_2} U_{Stabil} = 0.16V$ (AD-Wert: 32) - bei Dunkelheit
$ U_{a_{max}} = \frac{R_2}{R_1 + R_{LDR_{hell}} + R_2} U_{Stabil} = 3.3V$ (AD-Wert: 664) - bei Helligkeit

Somit werden gut $ 60\%$ des Wertebereiches des ADUs ausgenutzt.

Betrachtung der Meßergebnisse

[1cm]

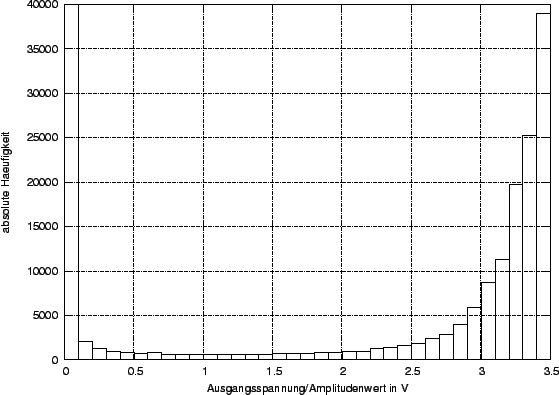
\begin{figure}\centerline{\epsffile{LDR.Histogramm.eps} }\end{figure}



Dieses Histogramm enthält alle Meßwerte welche in dem von mir bearbeiteten Zeitabschnitt gemessen wurden. Die Anzahl der 0-Werte wurde abgeschnitten um die restliche Verteilung besser darstellen zu können. Sie ist bei etwas über 111000 anzusiedeln.

Der errechnete Spannungsbereich stimmt mit dem tatsächlich gemessenem ziemlich gut überein. Anders als errechnet liegt die Ausgangsspannung bei abgedunkeltem LDR zwischen $ 0V$ und $ 0.1V$. Laut Rechnung wäre der Bereich zwischen $ 0.1V$ und $ 0.2V$ zu erwarten gewesen. Die maximale Ausgangsspannung, bei beleuchtetem LDR, liegt in dem Bereich von $ 3.4V$ bis $ 3.5V$. Zu erwarten war $ 3.2V$ bis $ 3.4V$.

Die entstandenen Abweichungen sind durch abweichende Angaben des $ R_{LDR}$ und Bauteiltoleranzen zu erklären.

Durch umstellen der oben genannten Formel kann der tatsächlich gemessene Widerstand des LDRs bestimmt werden (unter Vernachlässigung der Bauteiltoleranzen):

$ R_{LDR} = (\frac{U_{Stabil}}{U_a} - 1) R_2 - R_1$

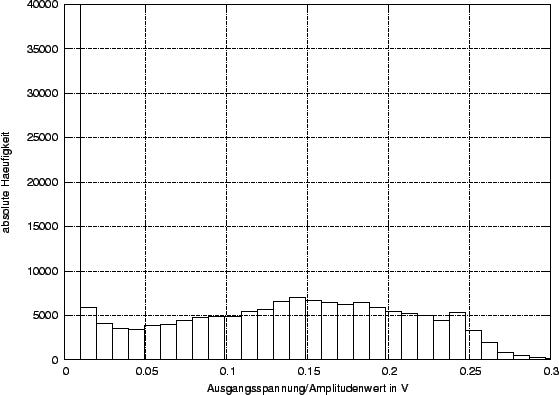
Die Verteilung ist folgendermaßen zu erklären:

Wird der LDR beleuchtet sinkt sein Widerstand sprunghaft von ca. $ 50k\Omega$ ($ 0.1V$) in einen Bereich von ca. $ 610\Omega$ ($ 2.5V$) bis ca. $ 270\Omega$ ($ 3V$). Von diesem Bereich aus sinkt der LDR dann langsam auf seinen Endwert von $ 27\Omega$ (3.5V). Der Abdunkelungsvorgang verläuft entsprechend Rückwärts. Da er nicht gleich auf den Endwert springt, ist er länger in dem niedrigeren Bereich, was dazu führt, dass mehr Meßwerte in diesem Bereicht liegen. Das vorhandensein von Meßwerten im Bereich von $ 50k\Omega$ ($ 0.1V$) bis $ 610\Omega$ ($ 2.5V$) ist mit der langsam ansteigenden Helligkeit morgens bzw. langsam abfallenden abends zu erklären.

Auswertung

Lichteinstrahlung über drei Tage (2. bis 4. April 2003)

Im folgenden wurde die Lichteinstrahlung vom 02.04.2003 00:00 bis zum 05.04.2003 00:00 betrachtet. Wie erwartet zeigen die Messungen, dass Licht von ca. 7 Uhr bis ca. 20 Uhr einstrahlte - dass es in diesem Zeitraum ``hell'' war. Das Diagramm zeigt die Leichteinstrahlung in Abhängigkeit von der Zeit. Die Lichteinstrahlung kann im Fall der Solarzelle näherungsweise als $ \frac{W}{m^2}$ angesehen werden, während die Skalierung der LDR-Kurve willkürlich ist.

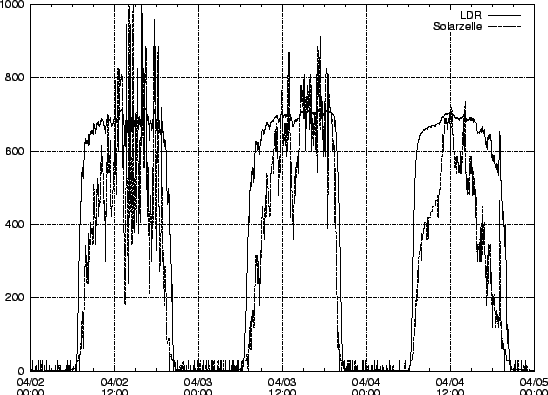
\begin{figure}\centerline{\epsffile{APRIL.licht.eps} }\end{figure}

Die Messung mit Hilft des LDRs ist erheblich träger als die mit der Solarzelle. Dies ist daran zu erkennen, dass die Kurve der Solarzelle im Vergleich zur LDR-Kurve erheblich springt. Jede vor die Sonne ziehende Wolke führt zu erheblichen Signalschwankungen. Des weiteren ist gut zu erkennen, dass der LDR schon bei geringer Lichteinstrahlung an seinen Endwert geht. Dies führt dazu, dass fast kein Unterschied zwischen einem sonnigen Tag (02.04.) und einem Dunklerem (04.04.) in seiner Kurve zu erkennen ist. Diese Eigenschaft lässt den LDR für die Messung der Einstrahlungsintensität unbrauchbar werden. Etwas überspitzt könnte man sagen, dass der LDR nur zwischen hell und dunkel unterscheidet.

Die Ausschläge der Solarzelle bei Nacht sind durch Restbeleuchtung (vom Mond, Straßenlaternen, verirrte Lichtstrahlen von z.B. Autoscheinwerfern) und Störeinstrahlungen zu erklären.

Betrachtung der Tageslängen eines Jahres

Im folgenden wurde die Entwicklung der Tageslängen über ein Jahr betrachtet. Es ist nochmal darauf hinzuweisen, dass es sich bei dem hier betrachteten Zeitraum um den vom 01.07.2002 bis zum 30.06.2003 handelt. Um die Tageslänge berechnen zu können, wurde der Werteverlauf des LDRs untersucht. Es wurde ein Schwellwert von 30 angenommen. Also wenn Wert größer 30 $ \Rightarrow$ hell, bzw. Wert $ <$ 30 $ \Rightarrow$ dunkel. Alle Meßwerte unter 500 Minuten sind unrealistisch und wurden aussortiert. Sie entstehen durch mehrmaliges durchschreiten des Schwellwertes.

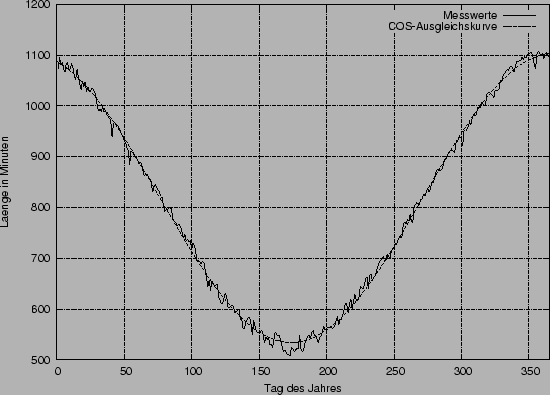
\begin{figure}\centerline{\epsffile{daylen.eps} }\end{figure}

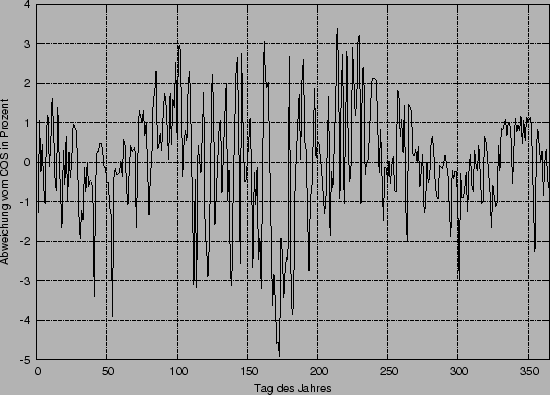
Besonders hervorzuheben ist die Tatsache, dass der Verlauf der Tageslängen einem Kosinus (hier $ Tageslaenge(Tag) = 819min + \cos(0.0161 Tag + 0.337)285min$) sehr gut entspricht. Wie sie in diesem Diagramm erkennen können, liegt die maximale relative Abweichung unter $ 5\%$. Der Mittelwert der Abweichung liegt bei $ -0.01\%$, der Mittelwert der vorzeichenlosen Abweichungen liegt bei $ 1.08\%$.

\begin{figure}\centerline{\epsffile{daylen.diff.eps} }\end{figure}

Quellen

Eine Beschreibung des Fernmesssystems, die Aufgabenstellungs sowie alle Meßwerte können hier runtergeladen bzw. eingesehen werden:

http://elgm01.fbe.hs-bremen.de/

Die Meßwerte in dem von mir bearbeitete Zeitraum sind hier zu finden:

ftp://elgm01.fbe.hs-bremen.de/pub/messung.0203.zip

Diese Dokument, sowie alle verwendeten Skripte können unter folgender URL eingesehen werden:

http://www.lgut.uni-bremen.de/an-h/fhs/EMT-L/FM_Hofmeier/

PDF Version LaTeX SRC

Pages by Andreas Hofmeier
 An-H
 eMail Impressum/Note Datenschutzerklärung
http[s]://www.abmh.de/fhs/EMT-L/FM_Hofmeier/FM.HTML/index.html
Creative Commons License
(c) Andreas B. M. Hofmeier
This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 Germany License
Andreas Hofmeier 2004-07-28